vcsharp2003
- 913
- 179
- Homework Statement
- What would be the potentials ##V_1## and ##V_2## on the surface of the concentric conducting shells shown in diagram?
- Relevant Equations
- Potential at a point ##r_1## due to a point charge ##q## is ##V_1=\frac {kq} {{r_1}}##
Each spherical shell will contribute to potential on the surface of inner shell and the same will apply to outer shell.
Due to inner shell ##V_1 = \frac {kQ} {{r_1}}## and due to outer shell ##V_1 = \frac {-kQ} {r_1}##. Therefore potential on inner surface is zero.
But the answers are ##V_1 = \frac {kQ} {{r_1}}## and ##V_2 = \frac {-kQ} {{r_2}}## .
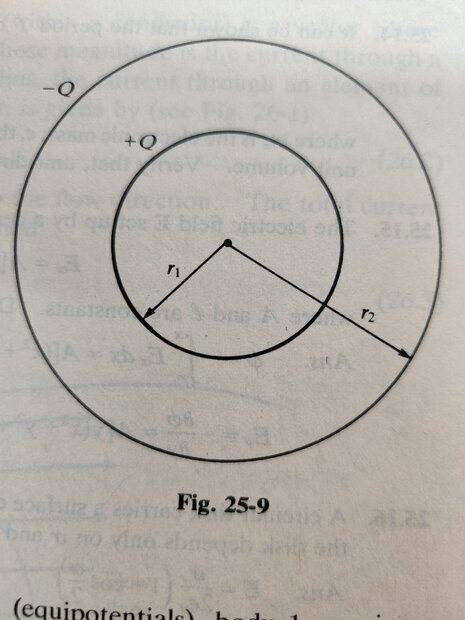
Due to inner shell ##V_1 = \frac {kQ} {{r_1}}## and due to outer shell ##V_1 = \frac {-kQ} {r_1}##. Therefore potential on inner surface is zero.
But the answers are ##V_1 = \frac {kQ} {{r_1}}## and ##V_2 = \frac {-kQ} {{r_2}}## .