evinda
Gold Member
MHB
- 3,741
- 0
Hi! (Mmm)
I am looking at Prim's algorithm:
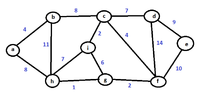
and..I want to apply it at this graph:
View attachment 3111
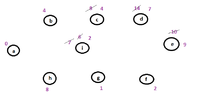
These are the keys that I found:
View attachment 3112
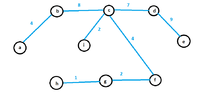
Is it right,or have I done something wrong? (Thinking)
Which vertices do I have to connect now,to get a minimum spanning tree? (Thinking)
I am looking at Prim's algorithm:
Code:
Prim(G,w,v)
for each u ϵ V
key[u]<-oo // the minimum of the weights of the edges,
that connect the vertex u with an other
vertex of the tree
p[u]<-∅
key[v]<-0
Q<-V // priority queue,the vertices are sorted,with respect to key[u]
while Q≠∅
u<-Εxtraction_of_minimum(Q)
for each v ϵ adj[u]
if v ϵ Q and w(u,v)<key[v] then
p[v]<-u
key[v]<-w(u,v)and..I want to apply it at this graph:
View attachment 3111
These are the keys that I found:
View attachment 3112
Is it right,or have I done something wrong? (Thinking)
Which vertices do I have to connect now,to get a minimum spanning tree? (Thinking)