Problem of the Week # 135 - October 27, 2014

[Ackbach]

Here's this week's problem!

-----

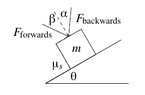
A block of mass $m$ lies on a ramp, and the coefficient of static friction between the block and the ramp is $\mu_s$. The ramp forms an angle $\theta$ from the horizontal. Assume that $\theta>\arctan(\mu_s)$ (i.e., assume that without any additional forces, the block would slide down the ramp).

(a) What is the maximum backwards angle $\alpha$ from the normal to the ramp that a constant pushing force of magnitude $F$ can make such that the block remains motionless?

(b) What is the maximum forwards angle $\beta$ from the normal to the ramp that a constant pushing force can make such that the block remains motionless? (For the forward case, assume $F$ is strong enough to move the block up the ramp if it was parallel to the ramp.)

https://www.physicsforums.com/attachments/3452._xfImport

-----

Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[Ackbach]

No one answered this week's problem. Here is my solution:

Spoiler

First we consider the backwards case.
We choose a tilted coordinate system, $y$ positive up and
perpendicular to the ramp, and $x$ positive up the ramp. A free-body
diagram yields that in the $x$ direction, Newton's Second Law
gives $\mu_s F_N-mg\sin(\theta)-F\sin(\alpha)=0$. Here $F_N$ is the
normal force. In the $y$ direction, we have
$F_N-F\cos(\alpha)-mg\cos(\theta)=0$. We solve the second equation for
$F_N=F\cos(\alpha)+mg\cos(\theta)$. Plugging this into the $x$
equation yields
\begin{align*}
0&=\mu_s [F\cos(\alpha)+mg\cos(\theta)]-mg\sin(\theta)-F\sin(\alpha) \\
\mu_s F \cos(\alpha)-F\sin(\alpha)&=mg\sin(\theta)-\mu_s mg\cos(\theta)\\
F[\mu_s\cos(\alpha)-\sin(\alpha)]&=mg[\sin(\theta)-\mu_s \cos(\theta)] \\
\sqrt{\mu_s^2+1} \, \sin(\alpha-\arctan(1/\mu_s))&=\frac{mg}{F}
\sqrt{\mu_s^2+1}\sin(\theta-\arctan(1/\mu_s)) \\
\sin(\alpha-\arctan(1/\mu_s))&=\frac{mg}{F}
\sin(\theta-\arctan(1/\mu_s)) \\
\alpha-\arctan(1/\mu_s)&=\arcsin\left[\frac{mg}{F}
\sin(\theta-\arctan(1/\mu_s))\right] \\
\alpha&=\arctan(1/\mu_s)+\arcsin\left[\frac{mg}{F}
\sin(\theta-\arctan(1/\mu_s))\right].
\end{align*}

Next, we consider the fowards case. This time, the friction force
is directed down the ramp, while the component of the force $F$ parallel
to the ramp is now directed up the ramp. Thus, the $x$ and $y$
equations become
\begin{align*}
F\sin(\beta)-\mu_s F_N-mg\sin(\theta)&=0, \; \text{and} \\
F_N-F \cos(\beta)-mg\cos(\theta)&=0,
\end{align*}
respectively. Solving for $\beta$ yields
$$\beta=\arctan(1/\mu_s)+\arcsin\left[\frac{mg}{F} \sin(\theta
+\arctan(1/\mu_s)) \right].$$