Lambda96
- 233
- 77
- TL;DR
- What does this notation ##A_{\quad i}^j## and ##A_i^{\quad j}## mean?
Hi,
In one of my assignments, we had to prove that the Frobenius product corresponds to a complex scalar product. For one, we had to prove that the Frobenius product is hermitian symmetric.
I have now received the solution to the problem, and unfortunately I do not understand the notation for the individual matrix elements. I only know the notation ##a_{ij}## but what does it mean when one of the indices is written with a space of A or B, what is this space about? What should be the row and what the column in this kind of notation?
Here is the solution
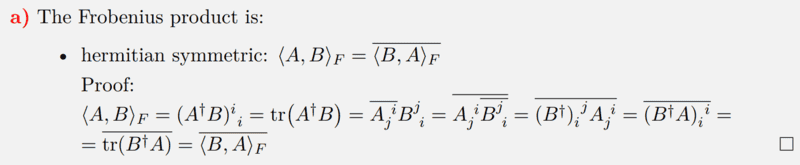
In one of my assignments, we had to prove that the Frobenius product corresponds to a complex scalar product. For one, we had to prove that the Frobenius product is hermitian symmetric.
I have now received the solution to the problem, and unfortunately I do not understand the notation for the individual matrix elements. I only know the notation ##a_{ij}## but what does it mean when one of the indices is written with a space of A or B, what is this space about? What should be the row and what the column in this kind of notation?
Here is the solution