Problem with reflection and transmission of waves

[LCSphysicist]

Homework Statement

I will post below an image.

Relevant Equations

There is no actually.

See, to illustrate:
Let's suppose there is an incoming wave by x < 0, what is the problem?

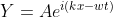
It will find a bead in the string, so:

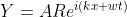, x < 0

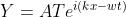, x > 0

T and R are the transmitted and reflected coefficients.

Now suppose there is another bead in x = L. The problem is what happens 0 < x < L:

The transmitted wave will be reflected in bead 2, so this reflected wave will be reflected again in the first bead, and so go on...
How to deal with this problem? We really need to deal with this series?

Y = A(T + TR + TRR + TRRR + TRRRR + ...)

(i am just excluding the complex therms to illustrate what i am really asking

notation:

T = transmitted by the first
TR = transmitted by the first, reflected by the second
TRR = transmitted by the first, reflected by the second, reflected by the first

 

[LCSphysicist]

The things become worst if we imagine a closed room, and a three dimensional wave... So i think i am missing something.

 

[hutchphd]

Your attachments were difficult to see, so I will pontificate.
The answer is yes you do:

1. The series need to keep track of phase (i.e. everything is complex)
2. It is usually trivial to sum and
3. it produces the resonance curve

I find it some of the most beautiful and simple physics that exists!

In 3D the problem can usually be separated according to symmetry. This gives rise to various solutions, often collectively called Fano resonances. i know (personally) of an excellent treatment of scattering from periodic atomic surfaces with an attractive potential.