ElectronicTeaCup
- 23
- 1
- TL;DR
- Show that the product of the distances from the foci to any point of any tangent to an ellipse is ##b^2##
where b is the semi-minor axis.
As part of the final stage of a problem, there is some algebraic manipulation to be done (from the solution manual):
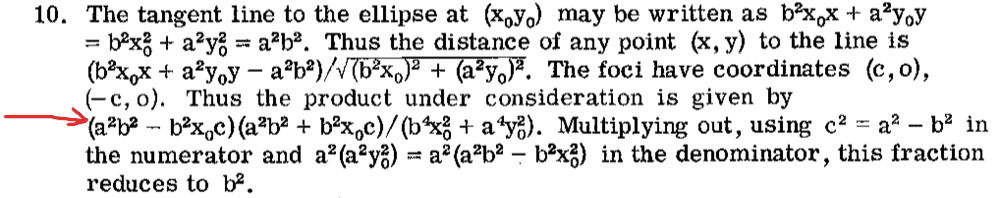
But I'm getting lost somewhere:
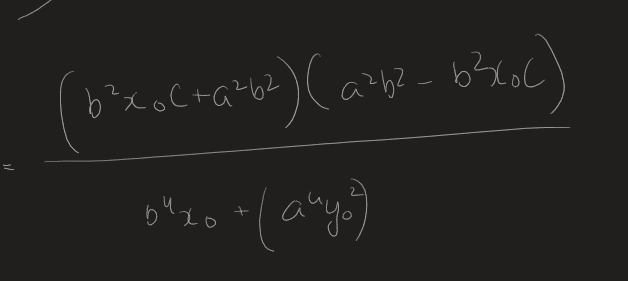
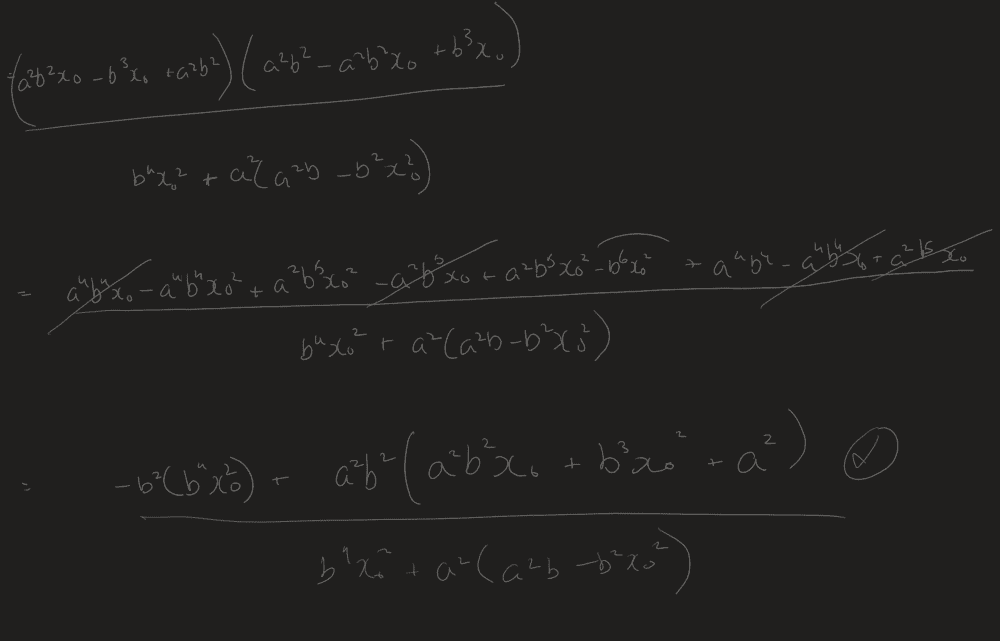
Also a bit of general advice needed: This is part of a self-study Calculus course, and I often have difficulty with bigger algebraic manipulations like this. I often feel if I made a deviation at some point, I will never be able to get to the solution—and I am assuming I need to go through all the possible ways before I have my solution. When in such a situation, I peek at the answer and force the solving into the direction of the solution. Is this bad practice? I feel I shouldn't be spending inordinate amounts of time on algebra in a calculus course.
But I'm getting lost somewhere:
Also a bit of general advice needed: This is part of a self-study Calculus course, and I often have difficulty with bigger algebraic manipulations like this. I often feel if I made a deviation at some point, I will never be able to get to the solution—and I am assuming I need to go through all the possible ways before I have my solution. When in such a situation, I peek at the answer and force the solving into the direction of the solution. Is this bad practice? I feel I shouldn't be spending inordinate amounts of time on algebra in a calculus course.