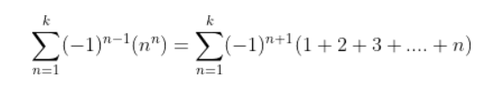Proof by induction? No Idea what I should do :(
Click For Summary
SUMMARY
The discussion focuses on proving the equation $$\sum_{n = 1}^k (-1)^{n - 1} n^2 = (-1)^{k + 1} \sum_{n = 1}^k n$$ by mathematical induction. Participants clarify that the initial attempts were incorrect, specifically noting that $n^n$ should be $n^2$. The correct approach involves simplifying the right side using the formula for the sum of the first $n$ integers, $$\sum_{n = 1}^k n = \frac{1}{2}k(k+1)$$. The proof is established by demonstrating that the equation holds for $k=1$ and then assuming it is true for $k$ to show it is also true for $k+1.
PREREQUISITES- Understanding of mathematical induction
- Familiarity with summation notation
- Knowledge of the formula for the sum of the first n integers
- Basic algebraic manipulation skills
- Study the principles of mathematical induction in detail
- Learn about summation techniques and identities
- Explore proofs involving sequences and series
- Practice problems on mathematical induction with varying complexity
Students in mathematics, educators teaching algebra and calculus, and anyone interested in understanding mathematical proofs and induction techniques.
Similar threads
- · Replies 3 ·
- · Replies 5 ·
- · Replies 4 ·
- · Replies 13 ·
- · Replies 4 ·
Undergrad
Question about mathematical induction
- · Replies 10 ·
- · Replies 6 ·
- · Replies 1 ·
- · Replies 13 ·
- · Replies 6 ·