Proof Logic: Proving w/o Truth Table?

[bobby2k]

Please take a look at this proof:

The thing I do not get is how they can do it so fast. If I were to prove this using a truth table, I would have to use 16 rows, because of all the possibilities, however they seem to not have to take into account a lot of the possibilities when they prove this.

For me it looks like they have assumed that:
\negB→C is TRUE
C→\negD is TRUE
D\veeO is TRUE
\negO is TRU

But how can they just do this?
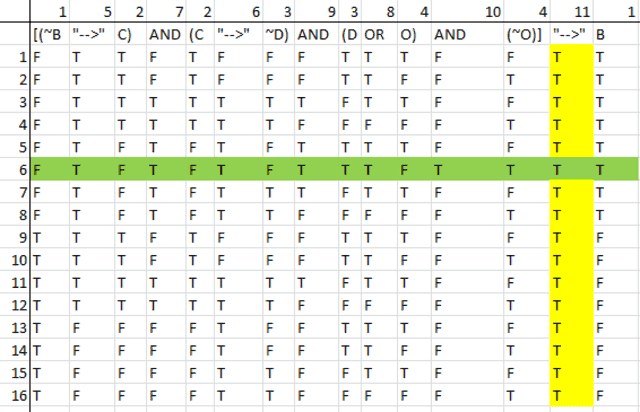
I made the truth table, am I correct to assume that the proof above, they only looked at row six in the truth table, many other possibilities were not considered? How can they just look away from these possibilities? Do you agree that they only considered row six in their proof?

 

[CompuChip]

Yes, because that is what the symbol "$\implies$" means: $[A_1 \wedge \cdots \wedge A_n] \implies B$ is true if assuming the A_i to be true leads to B necessarily being true. Whenever $A_1 \wedge \cdots \wedge A_n$ is not true, i.e. one or more of the A_i are false, $A \implies B$ is true by definition (check your truth table).

Alternatively, you can do a proof by contradiction: the statement is equivalent to $\not B \implies \not [A_1 \wedge \cdots \wedge A_n]$ (of course, you would have to prove this first, e.g. by making the truth tables of $A \implies B$ and $\not B \implies \not A$). However, you need to develop the logic a bit more formally to get that - in particular you need to introduce assumptions.

 

[gopher_p]

It appears as though you may be confused regarding the distinction between the \Rightarrow and \rightarrow symbols. In this context, \rightarrow is a symbol in the formal language that is being studied while \Rightarrow is a symbol in the metalanguage (the language used to study the formal language) used as shorthand for "B is a valid consequence of A". So A\rightarrow B is a proposition/sentence/well-formed formula of the formal language (whenever A and B are), while A\Rightarrow B is not.

Semantically the \rightarrow of the formal language turns out to "mean" approximately the same thing as the \Rightarrow of the metalanguage (which is likely the source of the confusion), but they really are very different symbols in this context. Formally, \rightarrow is just a binary connective with no "meaning"; i.e. it is equipped only with rules governing its usage in forming new propositions from old ones. It is given "meaning" by the logical tautologies chosen for the formal system. The same can be said for the other logical symbols; \lor, \land, and \lnot.

 

[bobby2k]

Yes, because that is what the symbol "$\implies$" means: $[A_1 \wedge \cdots \wedge A_n] \implies B$ is true if assuming the A_i to be true leads to B necessarily being true. Whenever $A_1 \wedge \cdots \wedge A_n$ is not true, i.e. one or more of the A_i are false, $A \implies B$ is true by definition (check your truth table).

Alternatively, you can do a proof by contradiction: the statement is equivalent to $\not B \implies \not [A_1 \wedge \cdots \wedge A_n]$ (of course, you would have to prove this first, e.g. by making the truth tables of $A \implies B$ and $\not B \implies \not A$). However, you need to develop the logic a bit more formally to get that - in particular you need to introduce assumptions.

Thanks, what I find confusing is when I can assume things to be true in a proof, and when it is not ok to assume things to be true in a proof.

It appears as though you may be confused regarding the distinction between the \Rightarrow and \rightarrow symbols. In this context, \rightarrow is a symbol in the formal language that is being studied while \Rightarrow is a symbol in the metalanguage (the language used to study the formal language) used as shorthand for "B is a valid consequence of A". So A\rightarrow B is a proposition/sentence/well-formed formula of the formal language (whenever A and B are), while A\Rightarrow B is not.

Semantically the \rightarrow of the formal language turns out to "mean" approximately the same thing as the \Rightarrow of the metalanguage (which is likely the source of the confusion), but they really are very different symbols in this context. Formally, \rightarrow is just a binary connective with no "meaning"; i.e. it is equipped only with rules governing its usage in forming new propositions from old ones. It is given "meaning" by the logical tautologies chosen for the formal system. The same can be said for the other logical symbols; \lor, \land, and \lnot.

Yes, it seems I have much confusion regarding those two. Which of them is used in Calculus? I mean there is a proof that says that if f is differentiable on (a,b) then f is continious on (a,b), is it supposed to be single or double arrow here?

 

[gopher_p]

Yes, it seems I have much confusion regarding those two. Which of them is used in Calculus? I mean there is a proof that says that if f is differentiable on (a,b) then f is continious on (a,b), is it supposed to be single or double arrow here?

In my experience, both versions are used as shorthand for the English words/phrases "implies" or "follows from" or "if ... then" in non-logic courses. Usage is very informal and somewhat imprecise; typically used by lecturers who are constrained by time from writing out the English words and authors too lazy to do so.

The usage of both symbols here is very formal and precise. In effect, they are used for different things here than what you have likely seen previously. It appears as though \Rightarrow is being used as shorthand for the (hopefully) well-defined term "valid consequence"; your text probably says something along the lines of "B is a valid consequence of A if B assumes a truth value of 1 whenever A assumes a truth value of 1". You should take this as the definition of that term/symbol in the context of the text. Don't try and impose on that term any previous understanding of what it means; it means only what author says it means. As I mentioned earlier, \rightarrow is almost universally reserved by logic texts as a symbol in a formal language. It technically has no meaning; only rules for how it can be used to build formulas in the language.

Keep in mind that one of the purposes of symbolic logic is to encode our intuitive notions of what logical reasoning should tell us into an unambiguous, easily manipulated language. The language is completely artificial. On its surface, it's just a bunch of squiggles and lines with no meaning. The rules governing the syntax (how formulas are built) and how truth value are assigned as well as the tautologies chosen are what allow us to use this language to do logic.

A bit of unsolicited advice: If you're by any chance studying this text in order to better understand the proofs in another course, you should stop. While you might learn something that helps, you're more likely (in my experience) to confuse yourself. A course/text in mathematical logic is designed for one who is already comfortable with understanding and determining what constitutes a logically valid argument.

Edit: Curiosity led me to seek out the text that was quoted. It looks like the section on logic is semi-formal, and much of what I have posted is not pertinent. I will say that from what I have read of that section, not much of it (in my opinion) is important to studying and understanding abstract mathematics.

 

[verty]

They don't look at all the possibilities because of the Law of the Excluded Middle: A or ~A. In (Aristotelian) logic, everything is either true or not true. If it can't be not true, it is true. Think of Sherlock Holmes' quip:

If you have eliminated the impossible, whatever remains, however improbable, must be the truth.

We can now understand what was meant by this.