- 13,404
- 4,176
- TL;DR
- I quote a passage from Wikipedia and ask a possibly dumb question about real numbers.
Here's a quote from here:
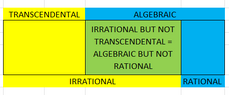
Here's my question. If transcendental numbers are all numbers that are not algebraic, how do we know that the disjoint union of the sets of algebraic numbers and transcendental numbers is exactly ##\mathbb R## and not an uncountable proper subset of it? (Here, I assume that ##\mathbb R## is defined as the completion of ##\mathbb Q##, or simply put, the disjoint union of the set of rational and irrational numbers).Properties
A transcendental number is a (possibly complex) number that is not the root of any integer polynomial. Every real transcendental number must also be irrational since every rational number is the root of some integer polynomial of degree one.[17] The set of transcendental numbers is uncountably infinite. Since the polynomials with rational coefficients are countable, and since each such polynomial has a finite number of zeroes, the algebraic numbers must also be countable. However, Cantor's diagonal argument proves that the real numbers (and, therefore also the complex numbers) are uncountable. Since the real numbers are the union of algebraic and transcendental numbers, it is impossible for both subsets to be countable. This makes the transcendental numbers uncountable.
Last edited: