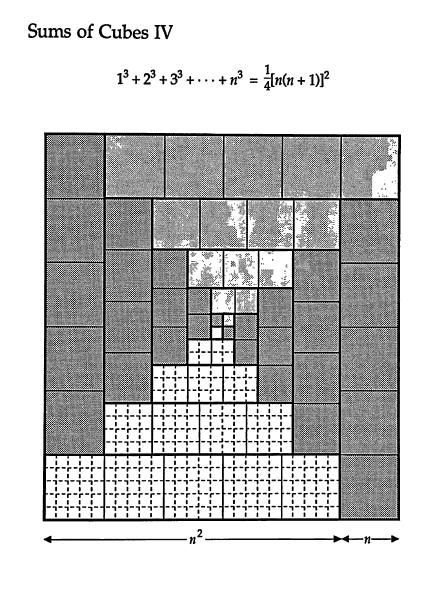
Discussion Overview
The discussion revolves around the proof of the formula for the sum of the cubes of the first T odd numbers, specifically the expression 1³ + 3³ + 5³ + ... + T³. Participants explore various methods of proof, including derivations and induction, while sharing their thoughts on the nature of mathematical proofs.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant presents the formula for the sum of cubes of odd numbers and requests a proof.
- Another participant expresses difficulty in completing the proof.
- A participant shares a solution involving a detailed algebraic manipulation leading to the conclusion that the sum equals T³.
- Some participants argue that deriving the result is more satisfying than using induction, while others prefer the simplicity of induction.
- Concerns are raised about the justification of certain proofs, with one participant noting that their proof only suggests a pattern rather than providing a complete proof.
- Several participants discuss the relationship between different mathematical concepts and the elegance of certain proofs, including references to number theory and properties of sums.
- One participant reflects on the complexity of using inductive reasoning and the challenges of finding initial answers.
Areas of Agreement / Disagreement
Participants express differing views on the preferred methods of proof, with some favoring derivations and others advocating for induction. There is no consensus on a single approach, and the discussion remains unresolved regarding the best method to prove the formula.
Contextual Notes
Some participants mention the limitations of their proofs, such as reliance on patterns or assumptions that have not been fully justified. The discussion also touches on the complexity of mathematical reasoning and the interplay between discrete and continuous methods.