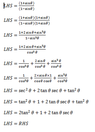Prove Identity: (1+sin(x))/(1-sin(x))=2tan^2(x)+1+2tan(x)sec(x)

  • Context: MHB 
  • Thread starter Thread starter Sean1
  • Start date Start date
  • Tags Tags
    Identity
Click For Summary
SUMMARY

The identity \(\frac{1+\sin(x)}{1-\sin(x)}=2\tan^2(x)+1+2\tan(x)\sec(x)\) can be proven by manipulating the left-hand side. By multiplying by the conjugate \(\frac{1+\sin(x)}{1+\sin(x)}\), the expression simplifies without fractions. This method effectively transforms the left-hand side into a form that can be compared with the right-hand side, confirming the identity's validity.

PREREQUISITES
  • Understanding of trigonometric identities, specifically tangent and secant functions.
  • Knowledge of algebraic manipulation techniques, including multiplying by conjugates.
  • Familiarity with the sine function and its properties.
  • Basic skills in simplifying rational expressions.
NEXT STEPS
  • Study the derivation of trigonometric identities using algebraic methods.
  • Learn about the properties of tangent and secant functions in trigonometry.
  • Explore techniques for simplifying complex fractions in trigonometric expressions.
  • Practice proving other trigonometric identities for deeper understanding.
USEFUL FOR

Students and educators in mathematics, particularly those focusing on trigonometry, as well as anyone looking to enhance their skills in proving mathematical identities.

Sean1
Messages
5
Reaction score
0
I cannot seem to prove the following identity

(1+sin(x))/(1-sin(x))=2tan^2(x)+1+2tan(x)sec(x)

Can you assist?
 
Mathematics news on Phys.org
Hi Sean,

Let's start with the left-hand side.

$$\frac{1+\sin(x)}{1-\sin(x)}$$.

We want this to turn into an expression without a fraction, so maybe we can try getting rid of the denominator somehow. When I see something in the form of $a-b$, I often try multiplying by the conjugate $a+b$.

$$\frac{1+\sin(x)}{1-\sin(x)} \left( \frac{1+\sin(x)}{1+\sin(x)} \right) $$

What do you get after trying this?
 
Thanks for getting me started.

This is my working. Can you confirm my approach is correct?

View attachment 4467
 

Attachments

  • identity solution.PNG
    identity solution.PNG
    2.9 KB · Views: 160
Last edited:
Looks good! :)
 

Similar threads

MHB Express cos(2 tan^-1(x/4)) and sin(2tan^-1(x/4) as an algebraic expression in x
  • · Replies 3 ·
Replies
3
Views
2K
MHB What is the Value of \(2\tan\frac{1}{2}A\tan\frac{1}{2}B\) in Triangle ABC?
  • · Replies 2 ·
Replies
2
Views
1K
MHB Can you prove the following two difficult trigonometric identities?
  • · Replies 3 ·
Replies
3
Views
1K
MHB Solving Trig Identity: Sin[1/2 sin^−1 (x)] = 1/2 X (sqr(1+x) –sqr(1-x))
  • · Replies 2 ·
Replies
2
Views
1K
High School How Do You Derive the Formula for sin(x-y)?
  • · Replies 5 ·
Replies
5
Views
2K
MHB Is this Trigonometric Expression a Constant Function of x?
  • · Replies 2 ·
Replies
2
Views
1K
MHB Trigonometric Question sin^2(180-x) cosec(270+x) + cos^2(360-x) sec(180-x)
  • · Replies 1 ·
Replies
1
Views
2K
High School Trigonometric Identity involving sin()+cos()
  • · Replies 11 ·
Replies
11
Views
2K
MHB Solving trig equation cos(x)=sin(x) + 1/√3
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad Transforming coordinates between Cartesian and spherical
  • · Replies 1 ·
Replies
1
Views
2K