- #1
- 3,634
- 1,511
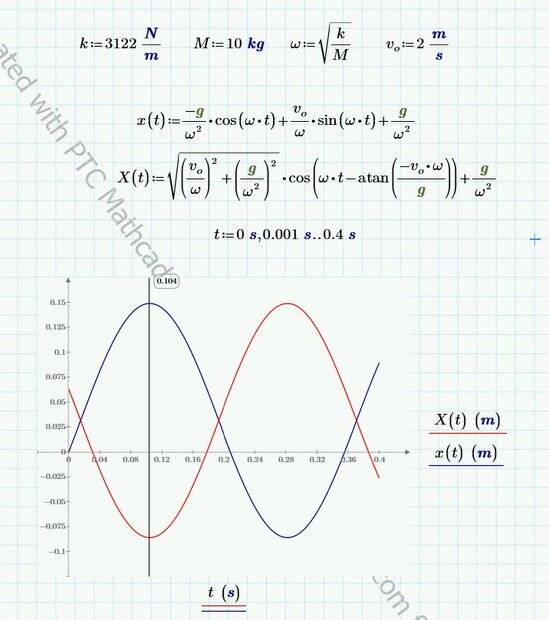
I'm trying to use the following trigonometric identity:
$$ a \cos ( \omega t ) + b \sin ( \omega t ) = \sqrt{a^2+b^2} \cos ( \omega t - \phi )$$ Where ##\phi = \tan^{-1} \left( \frac{b}{a} \right)## for the following equation:
$$ x(t) = -\frac{g}{ \omega^2} \cos ( \omega t) + \frac{v_o}{ \omega } \sin ( \omega t ) + \frac{g}{ \omega^2} $$
When I apply the identity I get:
##a = -\frac{g}{ \omega^2}##
##b = \frac{v_o}{ \omega }##
##\phi = \tan^{-1} \left( \frac{-v_o \omega}{g} \right)##
$$ X(t) = \sqrt{\left( \frac{g}{ \omega^2} \right)^2+\left( \frac{v_o}{ \omega } \right)^2} \cos \left( \omega t - \tan^{-1} \left( \frac{-v_o \omega}{g} \right) \right) + \frac{g}{ \omega^2} $$
However, on a plot they are not matching up...What am I doing wrong?
$$ a \cos ( \omega t ) + b \sin ( \omega t ) = \sqrt{a^2+b^2} \cos ( \omega t - \phi )$$ Where ##\phi = \tan^{-1} \left( \frac{b}{a} \right)## for the following equation:
$$ x(t) = -\frac{g}{ \omega^2} \cos ( \omega t) + \frac{v_o}{ \omega } \sin ( \omega t ) + \frac{g}{ \omega^2} $$
When I apply the identity I get:
##a = -\frac{g}{ \omega^2}##
##b = \frac{v_o}{ \omega }##
##\phi = \tan^{-1} \left( \frac{-v_o \omega}{g} \right)##
$$ X(t) = \sqrt{\left( \frac{g}{ \omega^2} \right)^2+\left( \frac{v_o}{ \omega } \right)^2} \cos \left( \omega t - \tan^{-1} \left( \frac{-v_o \omega}{g} \right) \right) + \frac{g}{ \omega^2} $$
However, on a plot they are not matching up...What am I doing wrong?