Prove the symmetry of an orbit from the given equation

[LCSphysicist]

Homework Statement:

How can i know that the orbit represented by the equation is symmetric with respect to two points?

Relevant Equations:

I will post an image below so it doesn't get confused

How can i know the resulting orbit of

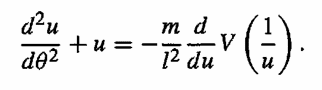is symmetric about two turning points?
Where m, l is constant.
V is function of r
u = 1/r
and

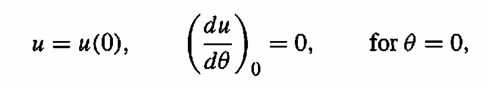
It is in polar coordinates.

We could show that varying theta from 0 to -θ will be the same if we vary 0 to Θ, but i don't know where to start

 

[epenguin]

Recognising symmetries is an essential and at the least saves unnecessary effort in maths and physics.
What you and everybody knows about planetary motion should give you some intuition though it is not indispensable here.
For a start, you do realize, you can see, that (du/dθ) at a point is necessary for symmetry about that point?
After that, first step, for there to be a symmetry of a function u =f(θ) at a point (u, θ) (where the slope is f'(θ) ), what does the slope have to be at -θ ? (Don't just look at symbols, draw yourself pictures.)

 

[LCSphysicist]

Recognising symmetries is an essential and at the least saves unnecessary effort in maths and physics.
What you and everybody knows about planetary motion should give you some intuition though it is not indispensable here.
For a start, you do realize, you can see, that (du/dθ) at a point is necessary for symmetry about that point?
After that, first step, for there to be a symmetry of a function u =f(θ) at a point (u, θ) (where the slope is f'(θ) ), what does the slope have to be at -θ ? (Don't just look at symbols, draw yourself pictures.)

About the second and first question

That's what i can imagine about symmetry in this case, the origin could be something like the focus, no?
opposite inclination

Actually i did this just with my intuition, so would need to prove.

 

[epenguin]

By symmetrical here is meant that the left is a reflection of the right. Well the way you have done the diagrams what should say top and bottom, but you might find it more Familiar and easier if you made θ the horizontal coordinate. In that case if the slope of the function of the origin is not 0, if it is 1 for example, can the function be symmetrical about that point? Join theParts of the curve as you have sketched into a continuous one. That is the preliminary point.
then get onto the second one I say above.

 

[LCSphysicist]

By symmetrical here is meant that the left is a reflection of the right. Well the way you have done the diagrams what should say top and bottom, but you might find it more Familiar and easier if you made θ the horizontal coordinate. In that case if the slope of the function of the origin is not 0, if it is 1 for example, can the function be symmetrical about that point? Join theParts of the curve as you have sketched into a continuous one. That is the preliminary point.
then get onto the second one I say above.

Hi, i am trying to understand, i see that in this case if the slope is different from zero, then traversing theta from 0 to 2pi, we would have something like

There is no possibility of assume any symmetry in this case about the orange point, right?

 

[epenguin]

I wouldn't agree - actually there is a symmetry of the kind we are looking for about the orange point and also any point on that line.

Can you just state a general condition for this kind of symmetry?

Forget about this particular problem for the moment and forget about the polar co-ordinates*. In Cartesian coordinates probably you have met examples of functions that were symmetrical between left and right about some point.
So for a function represented by y = f(x) can you state the general condition involving f for the graph to be symmetrical between left and right about the line x = 0? You may well have done exercises on that before.

*the co-ordinate system is immaterial really, but you are probably more used to Cartesian.

 

[LCSphysicist]

I wouldn't agree - actually there is a symmetry of the kind we are looking for about the orange point and also any point on that line.

Can you just state a general condition for this kind of symmetry?

Forget about this particular problem for the moment and forget about the polar co-ordinates*. In Cartesian coordinates probably you have met examples of functions that were symmetrical between left and right about some point.
So for a function represented by y = f(x) can you state the general condition involving f for the graph to be symmetrical between left and right about the line x = 0? You may well have done exercises on that before.

*the co-ordinate system is immaterial really, but you are probably more used to Cartesian.

A function is symmetric about x = 0 (or the axis Y) when the function f(x) satisfy the simple property:

f(x) = f(-x), like the reflection of a mirror. The function is called as even function.

It is really easier deal with cartesian

 

[epenguin]

Yes, and can you see that that is true in your diagram if you take your line to be the y axis? (Independently of where you place your y origin, I.e. the point you declare to be y = 0 ).

Can you now also see that for this symmetry about x = 0 , f'(0) = 0 necessarily?

Can you also see that these things are just as true for polar co-ordinates?

Given the property f(x) = f(-x) you mention, what can you then say about the first and second derivatives?

 

[LCSphysicist]

Yes, and can you see that that is true in your diagram if you take your line to be the y axis? (Independently of where you place your y origin, I.e. the point you declare to be y = 0 ).

Can you now also see that for this symmetry about x = 0 , f'(0) = 0 necessarily?

Can you also see that these things are just as true for polar co-ordinates?

Given the property f(x) = f(-x) you mention, what can you then say about the first and second derivatives?

"Yes, and can you see that that is true in your diagram if you take your line to be the y axis? (Independently of where you place your y origin, I.e. the point you declare to be y = 0 )."

Now i can see in a clear way your statement :)

"Given the property f(x) = f(-x) you mention, what can you then say about the first and second derivatives?"

We can use the chain rule, we would obtain [derivative with respect to x]
f'(x) = -f'(-x)
f''(x) = +f''(-x)

The first derivative of one is the opposite of the other,
and, by the second derivative, we can know that their concavity coincides very well

"Can you also see that these things are just as true for polar co-ordinates?"
Since we are just changing the coordinates system, and not the figure, i would agree.


"Can you now also see that for this symmetry about x = 0 , f'(0) = 0 necessarily?"

Yes, if the derivative exist, so it should be.