Prove the trigonometry identity and hence solve given problem

[chwala]

Homework Statement

Prove that $\csc ∅ - \cot ∅ = \tan \dfrac {∅}{2}$. Hence, deduce that $\tan \dfrac {π}{8} = \sqrt{2} -1$ and find $\tan \dfrac {3π}{8}$ in terms of $a+ b\sqrt{2}$

Relevant Equations

Trigonometry.

Refreshing on trig. today...a good day it is...ok find the text problem here; With maths i realize one has to keep on refreshing at all times... my target is to solve 5 questions from a collection of 10 textbooks i.e 50 questions on a day-day basis...motivation from late Erdos ...( pure math, applied, stats, mechanics} each and every day starting today...i will only post the interesting questions...

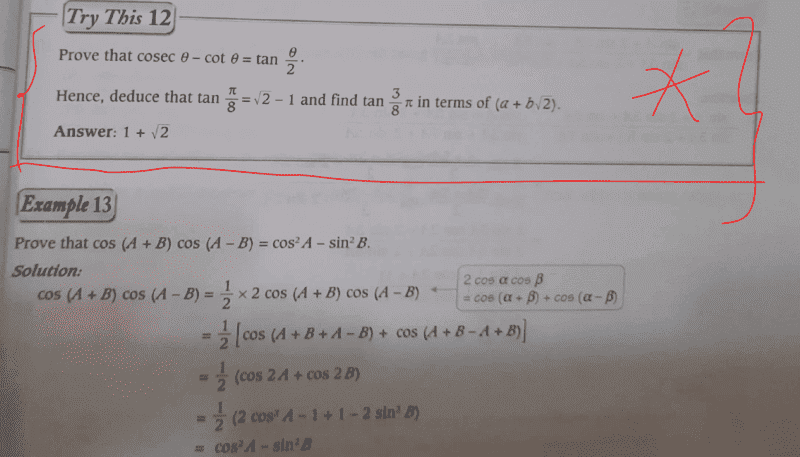
Ok my approach; let $\tan \dfrac{∅}{2}=t$

$\dfrac{1}{\sin ∅} - \dfrac{\cos∅ }{\sin ∅}=t$

$\dfrac{1-\cos ∅}{\sin ∅}=t$

$\dfrac{1+t^2-(1-t^2)}{1+t^2} ⋅\dfrac{1+t^2}{2t}=t$ thus true.

for second part;

Let $\dfrac{∅}{2}=\dfrac{π}{8}$

it follows that $∅ = \dfrac{π}{4}$

therefore; $\dfrac{1}{\sin \dfrac{1}{4} π} - \dfrac{\cos\dfrac{1}{4}π }{\sin \dfrac{1}{4}π}$=$\sqrt{2}$ $-\dfrac {1}{\sqrt{2}}$ ⋅$\sqrt{2}$= $\sqrt{2}-1$

Lastly;

$\tan \dfrac{3π}{8}= \tan \dfrac{π}{4} +\tan \dfrac{π}{8}$

=$\dfrac{\tan \dfrac{π}{4} +\tan \dfrac{π}{8}}{1-\tan \dfrac{π}{4} ⋅\tan \dfrac{π}{8}}$

=$\dfrac{1+\sqrt{2}-1}{1-\sqrt{2}+1}$

= $\dfrac{\sqrt{2}}{2-\sqrt{2}}$ ⋅ $\dfrac{2+\sqrt{2}}{2+\sqrt{2}}$

=$\dfrac{2+2\sqrt{2}}{2}= 1+\sqrt{2}$

Of course i know there might be a slightly different approach...would appreciate any comments. Cheers guys!

 

[Mark44]

Ok my approach; let $\tan \dfrac{∅}{2}=t$

$\dfrac{1}{\sin ∅} - \dfrac{\cos∅ }{\sin ∅}=t$

You're assuming what you intend to prove. The only time this is a reasonable approach is when all of the subsequent steps are reversible; i.e., one-to-one operations.

Since you haven't shown that all of your applied operations are one-to-one, a better way is to start with the expression on one side, and then manipulate it to get a sequence of equal expressions that eventually are equal to the other side of the equation you want to prove.

$\dfrac{1-\cos ∅}{\sin ∅}=t$

$\dfrac{1+t^2-(1-t^2)}{1+t^2} ⋅\dfrac{1+t^2}{2t}=t$ thus true.

It's not at all obvious to me how the left side above is equal to ${1 - \cos(\theta)}{\sin(\theta)}$.
If in fact they are equal, then you have proved that t = t, which is trivial.

for second part;

Let $\dfrac{∅}{2}=\dfrac{π}{8}$

it follows that $∅ = \dfrac{π}{4}$

therefore; $\dfrac{1}{\sin \dfrac{1}{4} π} - \dfrac{\cos\dfrac{1}{4}π }{\sin \dfrac{1}{4}π}$=$\sqrt{2}$ $-\dfrac {1}{\sqrt{2}}$ ⋅$\sqrt{2}$= $\sqrt{2}-1$

Lastly;

$\tan \dfrac{3π}{8}= \tan \dfrac{π}{4} +\tan \dfrac{π}{8}$

=$\dfrac{\tan \dfrac{π}{4} +\tan \dfrac{π}{8}}{1-\tan \dfrac{π}{4} ⋅\tan \dfrac{π}{8}}$

=$\dfrac{1+\sqrt{2}-1}{1-\sqrt{2}+1}$

= $\dfrac{\sqrt{2}}{2-\sqrt{2}}$ ⋅ $\dfrac{2+\sqrt{2}}{2+\sqrt{2}}$

=$\dfrac{2+2\sqrt{2}}{2}= 1+\sqrt{2}$

Of course i know there might be a slightly different approach...would appreciate any comments. Cheers guys!

 

[pasmith]

I would start from $$\begin{split} \cos \theta &= 1 - 2\sin^2(\theta/2) \\ \sin \theta &= 2\cos(\theta/2)\sin(\theta/2) \end{split}$$ and substitute these into $$\csc\theta - \cot\theta = \frac{1 - \cos \theta}{\sin \theta}.$$

 

[chwala]

You're assuming what you intend to prove. The only time this is a reasonable approach is when all of the subsequent steps are reversible; i.e., one-to-one operations.

Since you haven't shown that all of your applied operations are one-to-one, a better way is to start with the expression on one side, and then manipulate it to get a sequence of equal expressions that eventually are equal to the other side of the equation you want to prove.
It's not at all obvious to me how the left side above is equal to ${1 - \cos(\theta)}{\sin(\theta)}$.
If in fact they are equal, then you have proved that t = t, which is trivial.

Noted @Mark44 ... Ok we can have;

$\dfrac{1-\cosθ}{\sin θ}=\dfrac{\sin \dfrac{θ}{2}}{cos \dfrac{θ}{2}}$

We know from;

$\cos 2θ =\cos^2θ-\sin^2 θ$

$\cos 2θ =1-2\sin^2 θ$ , therefore it follows that;
$\cos θ = 1- 2\sin^2 \dfrac{1}{2}θ$

Also from $\sin 2θ=2\sin θ \cos θ$, We shall have
$\sin θ = 2 \sin \dfrac{1}{2}θ \cos \dfrac{1}{2}θ$

therefore,

$\dfrac{1-\cosθ}{\sin θ}=\dfrac{1-(1-2\sin^2 \dfrac{1}{2}θ)}{\sin θ}=\dfrac{2\sin^2 \dfrac{1}{2}θ}{2 \sin \dfrac{1}{2}θ \cos \dfrac{1}{2}θ}=\dfrac{\sin \dfrac{θ}{2}}{cos \dfrac{θ}{2}}=\tan \dfrac{θ}{2}$

 

[SammyS]

I would start from $$\begin{split} \cos \theta &= 1 - 2\sin^2(\theta/2) \\ \sin \theta &= 2\cos(\theta/2)\sin(\theta/2) \end{split}$$ and substitute these into $$\csc\theta - \cot\theta = \frac{1 - \cos \theta}{\sin \theta}.$$

Great idea !

 

[chwala]

From my university notes; i just noted that we could also use Euler approach and binomal formula for $\cos 2θ$ and $\sin2θ$ ; i.e

$\cos 2θ+ i \sin 2∅= (\cos θ+ i \sin ∅)^2=\cos^2θ+ _2C_1⋅i\cos θ\sinθ+ _2C_2⋅i^2\sin^2 θ$

where;

$\cos 2θ=\cos^2θ+_2C_2⋅i^2\sin^2 θ= \cos^2θ-\sin^2θ$ and

$i\sin 2θ=_2C_1⋅i\cos θ\sinθ$

$⇒\sin 2θ=2\sin θ\cos θ$

Bingo!