anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
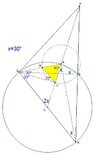
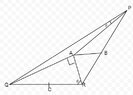
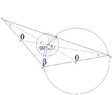
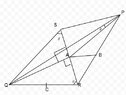
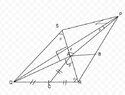
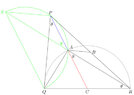
Let $PQR$ be a triangle and let $A$ be an interior point such that $\angle QAR=90^{\circ}$, $\angle QBA=\angle QRA$.
Let $B,\,C$ be the midpoints of $PR,\,QR$ respectively. Suppose $QA=2AB$, prove that $P,\,A,\,C$ are collinear.
Let $B,\,C$ be the midpoints of $PR,\,QR$ respectively. Suppose $QA=2AB$, prove that $P,\,A,\,C$ are collinear.