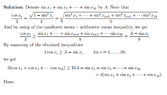SUMMARY
The discussion centers on proving the inequality \(\frac{\sum_{i=1}^{10}\cos x_i}{\sum_{j=1}^{10}\sin x_j} \ge 3\) under the condition that \(x_1, x_2, \ldots, x_{10} \in [0, \frac{\pi}{2}]\) and \(\sum_{i=1}^{10}\sin^2 x_i = 1\). Participants, including Albert, provided solutions and alternative approaches to this mathematical problem. The consensus highlights the importance of trigonometric identities and inequalities in establishing the proof.
PREREQUISITES
- Understanding of trigonometric functions, specifically sine and cosine.
- Familiarity with inequalities, particularly Cauchy-Schwarz inequality.
- Knowledge of the properties of angles in the interval \([0, \frac{\pi}{2}]\).
- Ability to manipulate summations and apply mathematical proofs.
NEXT STEPS
- Study the Cauchy-Schwarz inequality and its applications in trigonometry.
- Explore advanced trigonometric identities relevant to inequalities.
- Learn about the properties of functions defined on the interval \([0, \frac{\pi}{2}]\).
- Investigate alternative proofs for inequalities involving sums of trigonometric functions.
USEFUL FOR
Mathematicians, students studying advanced calculus or analysis, and anyone interested in inequalities involving trigonometric functions.