Discussion Overview
The discussion revolves around determining whether a given graph is planar or nonplanar, focusing on methods for proving planarity, including the use of specific graph properties and simplifications. Participants explore both theoretical and practical approaches to the problem, including software tools.
Discussion Character
- Homework-related
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
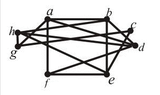
- One participant notes that the graph satisfies the inequality $$e \leq 3v - 6$$ and has a chromatic number of 4, suggesting it may be planar, but also mentions the presence of vertices of degree 4 or above, indicating a potential for nonplanarity.
- Another participant suggests that the graph may be reducible to $$K_5$$ but has not verified this claim.
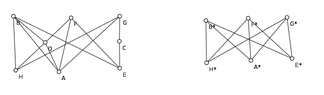
- A different participant asserts that the graph is non-coplanar and provides a series of simplifications that lead to a graph isomorphic to $$K_{3,3}$$, arguing that this implies the original graph is also non-coplanar.
- Some participants express uncertainty about whether the process of proving planarity is primarily trial-and-error or if there are more systematic methods available.
- One participant mentions using software (CaRMetal) to assist in visualizing and manipulating the graph, which they found helpful in identifying the nonplanarity.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best method for proving planarity or nonplanarity. There are competing views on whether the graph can be reduced to known nonplanar graphs, and the discussion includes both supportive and questioning perspectives on the approaches taken.
Contextual Notes
Some participants highlight the limitations of their approaches, including the reliance on specific graph properties and the challenges of visualizing complex graphs without software tools. There is also mention of the need for further verification of claims regarding reducibility to $$K_5$$ or $$K_{3,3}$$.