Proving Set Equivalence with Set Differences?

[A.Magnus]

View attachment 8555​

I am working on a set equivalent (the textbook refers as "equinumerous" denoted by ~) as follows:

If $S$ and $T$ are sets, prove that if $(S\backslash T) \sim (T\backslash S)$, then $S \sim T$.​

Here is my own proof, I am posting it here wanting to know if it is valid. (It may not be as elegant as the textbook's proof though.)

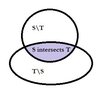
(1) We do not consider the cases of $S \subseteq T$, $T \subseteq S$ or $S \cap T = \emptyset$ since they lead to trivial solutions. We consider only the case where $S \cap T \ne \emptyset$. See the Venn diagram above.
(2) $(S \backslash T) \sim (T \backslash S)$ implies the existence of bijection $f: (S\backslash T) \to (T\backslash S)$. Here we need to prove the existence of bijection $g: S \rightarrow T$ to show $S \sim T$.
(3) Looking at the diagram, we need to prove only the existence of bijection $h: (S \cap T) \rightarrow T$ in order to prove the existence of bijection $g: S \rightarrow T$, since the bijection $f: (S \backslash T) \rightarrow (T \backslash S)$ is given.
(4) For all $x \in S \cap T,$ we have $ x \in S$ and $x \in T$. Hence the function $h: (S \cap T) \rightarrow T$ is in fact $h: T \rightarrow T$, which is an identity function. Since by textbook's theorem an identity function is always bijective, therefore $h: (S \cap T) \rightarrow T$ is indeed bijective.
(5) Hence there exists bijection $g: S \rightarrow T$, implying that $S \sim T$, as desired.

Thank you so much for your time and gracious help. ~MA

 

[Evgeny.Makarov]

Let $S=\{1,2\}$ and $T=\{2,3\}$. Then $S\cap T=\{2\}$. But the identity function from $S\cap T$ to $T$ is not a bijection, since these sets have different number of elements.

Also, strictly speaking a function $f:A\to B$ is a triple $(f,A,B)$ where $f\subseteq A\times B$ satisfying a couple of properties. In this sense one cannot arbitrarily change the function domain $A$. So saying "The function $h:S\cap T\to T$ is in fact $h:T\to T$" is inaccurate.

 

[Olinguito]

You have a bijection $f:(S\setminus T)\to(T\setminus S)$; you need to extend it to a function $F:S\to T$. The obvious candidate is the following:
$$F:S\to T;\ F(x)=\begin{cases}f(x) &\text{if}& x\in S\setminus T, \\\\ x &\text{if}& x\in S\cap T.\end{cases}$$
All you need to do now is to prove that $F:S\to T$ is a bijection.

 

[A.Magnus]

Let $S=\{1,2\}$ and $T=\{2,3\}$. Then $S\cap T=\{2\}$. But the identity function from $S\cap T$ to $T$ is not a bijection, since these sets have different number of elements.

Also, strictly speaking a function $f:A\to B$ is a triple $(f,A,B)$ where $f\subseteq A\times B$ satisfying a couple of properties. In this sense one cannot arbitrarily change the function domain $A$. So saying "The function $h:S\cap T\to T$ is in fact $h:T\to T$" is inaccurate.

Thank you for your time. Apparently my logic was flawed. ~MA

 

[A.Magnus]

You have a bijection $f: (S\setminus T)\to(T\setminus S)$; you need to extend it to a function $F:S\to T$. The obvious candidate is the following:
$$F:S\to T;\ F(x)=\begin{cases}f(x) &\text{if}& x\in S\setminus T, \\\\ x &\text{if}& x\in S\cap T.\end{cases}$$

All you need to do now is to prove that $F:S\to T$ is a bijection.

Thank you again for pointing this function out. The easiest way I can think of proving $F$ is bijective is by showing that both $F$ and $F^{-1}$ is injective. Is there any other simpler way? Thank you again for your time and gracious helps. ~MA

 

[Evgeny.Makarov]

The easiest way I can think of proving $F$ is bijective is by showing that both $F$ and $F^{-1}$ is injective.

What do you mean by $F^{-1}$?

 

[A.Magnus]

What do you mean by $F^{-1}$?

Opps! I don't understand why my mind strayed off. I am sorry. Let's do these:

(a) If $x \in S \backslash T$, the $f: (S \backslash T) \rightarrow (T \backslash S)$ is given as bijection by the problem.
(b) If $x \in S \cap T$ on the other hand, the $F(x) = x$ is an identity function and therefore it is a bijection. Hence $F(X)$ is a bijection.

Let me know and thank you again for all your times and gracious helps. ~MA

 

[Evgeny.Makarov]

Opps! I don't understand why my mind strayed off.

I didn't mean to say that $F^{-1}$ is out of place in this context. I just wanted to point out that inverse function may have slightly different definitions, and I was wondering what statement exactly regarding inverse functions you were using to show that $F$ is bijections. A potential complication is that one of the definitions allows $F^{-1}$ only when $F$ is already proven to be a bijection.

(a) If $x \in S \backslash T$, the $f: (S \backslash T) \rightarrow (T \backslash S)$ is given as bijection by the problem.
(b) If $x \in S \cap T$ on the other hand, the $F(x) = x$ is an identity function and therefore it is a bijection.

I agree.

Hence $F(X)$ is a bijection.

What statement are you using to justify this conclusion? The fact that you are trying to prove is rather simple, so the proof should be detailed. I think you made a leap here that is somewhat more than the intended level of detail allows.

I recommend using the definition of bijection to prove that $F$ is one.

 

[Olinguito]

This is how I would do the problem (it may be the same solution as the one in your textbook).

$$F:S\to T;\ F(x)=\begin{cases}f(x) &\text{if}& x\in S\setminus T, \\\\ x &\text{if}& x\in S\cap T.\end{cases}$$

First, prove that $F$ is injective. Note that as $T\setminus S$ and $S\cap T$ are disjoint, we have that for any $x\in S$, $F(x)\in T\setminus S\ \iff\ x\in S\setminus T$ (and similarly $F(x)\in S\cap T\ \iff\ x\in S\cap T$). Suppose $F(x_1)=F(x_2)$, $x_1,x_2\in S$. If $F(x_1),F(x_2)\in T\setminus S$, then $x_1,x_2\in S\setminus T$ and so $f(x_1)=F(x_1)=F(x_2)=f(x_2)$ and so, as $f$ is injective, we have $x_1=x_2$. If $F(x_1),F(x_2)\in S\cap T$, then $x_1,x_2\in S\cap T$ and so $x_1=F(x_1)=F(x_2)=x_2$. Hence $F$ is injective.

Now prove it’s surjective. Let $y\in T$. If $y\in T\setminus S$, then $y=f(x)$ for some $x\in S\setminus T$, by surjectivity of $f$, whence $y=f(x)=F(x)$. If $y\in S\cap T$, then $y=F(y)$. This shows that $F$ is surjective. QED.

 

[Evgeny.Makarov]

Some $S\setminus T$ (at least three) have to be changed to $T\setminus S$.