Pyrite roasting -- Mass balance with chemical reaction

[MexChemE]

Homework Statement

A certain pyrite ore contains 85% of FeS₂ and 15% of inerts. This ore is introduced into a roasting furnace with 20% excess air, in order to oxidize the FeS₂ in the reaction:
$$\textrm{FeS}_2 + \frac{11}{4}\textrm{O}_2 \rightarrow \frac{1}{2}\textrm{Fe}_2 \textrm{O}_3 + 2\textrm{SO}_2$$
The solid product contains 2% FeS₂ in mass. Using 100 lb as basis, determine:
a) The chemical equation describing the process using the calculation basis, in mass and mole.
b) Conversion percentage.
c) The volume of the exhaust gases at 300 °C and 1 atm.
d) The amount of solid product obtained.
e) The amount of sulfuric acid which can be formed from the exhaust gases.

Homework Equations

Steady state mass balance with chemical reaction
$$\textrm{In} + \textrm{Generation} = \textrm{Out} + \textrm{Consumption}$$

The Attempt at a Solution

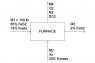
First, I sketched a diagram of the process, as you can see in the attachments. Now, here's my work.
Part a)
85 lb (0.708 lbmol) of FeS₂ are being fed into the furnace. So, here's the balanced equation in molar base:
$$0.708\textrm{FeS}_2 + 1.947\textrm{O}_2 \rightarrow 0.354\textrm{Fe}_2 \textrm{O}_3 + 1.416\textrm{SO}_2$$
And mass base:
$$85\textrm{FeS}_2 + 62.3\textrm{O}_2 \rightarrow 56.6\textrm{Fe}_2 \textrm{O}_3 + 90.6\textrm{SO}_2$$

Part b)
Now, for part b) I need to know how much FeS₂ reacted (in lb). We'll call this quantity "A." We now also know that the O₂ required is 1.947 lbmol. Assuming dry air (21% oxygen; 79% nitrogen), the moles of air required are 9.271 lbmol; and since we have a 20% of excess air, the air fed into the furnace is 11.125 lbmol, of which 2.336 lbmol are oxygen (74.76 lb). Now, we'll analyze the mass exchange occurring with the reaction. We know 85 lb of FeS₂ and 74.76 lb O₂ were fed into the furnace. If A lb of FeS₂ reacted, we will have an output of:
(85 - A) FeS₂
(74.76 - 0.73A) O₂
(0.67A) Fe₂O₃
(1.07A) SO₂
We know M₃ is composed of 15 lb of inerts plus some amount of iron sulphide and ferric oxide.
$$M_3=15+(85-A) + 0.67A= 100-0.33A$$
Now, if we perform a sulphide balance we have:
$$85 = A + 0.02M_3$$
Now we have a 2x2 linear equation system which we cal solve in order to obtain M₃ and A.
A = 83.551 lb
M₃ = 72.428 lb
The percentage of conversion will be given by:
$$\% \textrm{Conversion} = \frac{83.551}{85} \times 100\% = 98.3\%$$

Part c)
Now that we know A, we can calculate the amount of moles of exhaust gases, which is 10.616 lbmol. Assuming ideal beahvior, at 300 °C and 1 atm of pressure, the exhaust gases occupy a volume of 7997.3 ft³.

Part d)
The solid product is M₃, which are 72.428 lb, with a composition of:
(15 lb) Inerts
(1.499 lb) FeS₂
(55.979 lb) Fe₂O₃

Part e)
I have some doubts about my procedure for this part. We have 1.397 lbmol of SO₂, of which only 0.8604 lbmol can react with the limited amount of O₂ moles in the exhaust gases (which are 0.4302 lbmol) to form 0.8604 lbmol of SO₃. This amount of SO₃ will in turn react with a stoichiometric amount of water in order to produce 0.8604 lbmol of H₂SO₄.
Therefore, with an output of 1.397 lbmol of SO₂ and 0.4302 lbmol of O₂ as limiting reactant, 0.8604 lbmol of H₂SO₄ can be produced.

My concerns are mostly focused on part e), but feel free to point out any inconsistencies you may find along the way. Thanks in advance for any input!

 

[Borek]

It is not clear to me what the e asks. Process of producing sulfuric acid requires several steps and at least one additional reagent (water). If you can add water, why can't you use more air to oxidize all sulfur to SO₃?

 

[MexChemE]

You have a good point; if I took the freedom of adding water I could just add more air and oxidize the 1.397 lbmol of SO₂, and because of stoichiometry, that amount will produce 1.397 lbmol of H₂SO_4.. I originally used the limited amount of oxygen because the problem asked to use the product gases, but actually the only product gas of interest is SO₂. Also, the reaction SO₃ + H₂O is not very common in industry, it releases too much heat, as far as I know. So there's that little detail too.