lemon
- 199
- 0
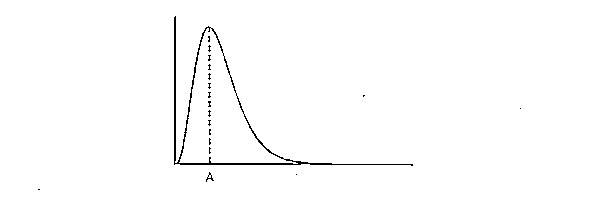
The discussion focuses on evaluating a mathematical problem involving turning points and coordinates, specifically the function 2x³e⁻ˣ. The user incorrectly applies the product rule and misinterprets the evaluation of the function at specific points. The correct evaluations yield turning points at (0, 0) and (3, ~2.7), with the second derivative providing insights into the concavity of the function. The user is advised to clarify their expressions and ensure they accurately represent the relationships between derivatives and function evaluations.
PREREQUISITESStudents studying calculus, mathematics educators, and anyone seeking to improve their understanding of function analysis and derivative applications.
lemon said:1. Hi. I have a part completed question. part a done. but not sure if correct. could someone check before i go onto part b please. thanks[/b
2. Homework Equations in image
3. The Attempt at a Solution in image