luke8ball
- 22
- 0
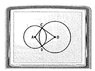
Hi Guys! I've attached a picture of the setup if you don't have Geometer's Sketchpad software. I honestly have no idea where to begin with this problem, as I've been staring at it for hours. Nevertheless, I've still put some thoughts down on what I think I should do.
Use Geometer’s Sketchpad and draw points A, B, C (not all three are collinear).
Construct segments AC and BC.
Draw circle with center A and radius AC
Draw circle with Center B and radius BC
Label the other intersection of the circles D.
Draw segments BD and AD.
a. Drag point A, B, C, or D to change the shape of ABCD. What types of quadrilaterals can be formed? Explain.b. Are there types of quadrilaterals that cannot be formed? List and explain.
Square – Yes. If the two circles have radii of the same length, and if you adjust points C and D accordingly, you can have all 90° angles.
Rectangle – You can have a rectangle with all equal sides, but you can’t have a rectangle that isn’t a square, as the adjacent sides are always radii of the same circle, and cannot be different lengths.
Rhombus – You can have a rhombus because you can have a square, and you could just adjust the angles if you wanted a rhombus that wasn’t a square?
Parallelogram – You can have a parallelogram, but it has to be a rhombus as well, because adjacent sides must be equal.
Kite – You can certainly have a kite, as the pairs of adjacent sides (radii) will always be equal.
Any hints would be truly appreciated; I feel like an idiot staring at this problem in Geometer's Sketchpad.
Homework Statement
Use Geometer’s Sketchpad and draw points A, B, C (not all three are collinear).
Construct segments AC and BC.
Draw circle with center A and radius AC
Draw circle with Center B and radius BC
Label the other intersection of the circles D.
Draw segments BD and AD.
a. Drag point A, B, C, or D to change the shape of ABCD. What types of quadrilaterals can be formed? Explain.b. Are there types of quadrilaterals that cannot be formed? List and explain.
The Attempt at a Solution
Square – Yes. If the two circles have radii of the same length, and if you adjust points C and D accordingly, you can have all 90° angles.
Rectangle – You can have a rectangle with all equal sides, but you can’t have a rectangle that isn’t a square, as the adjacent sides are always radii of the same circle, and cannot be different lengths.
Rhombus – You can have a rhombus because you can have a square, and you could just adjust the angles if you wanted a rhombus that wasn’t a square?
Parallelogram – You can have a parallelogram, but it has to be a rhombus as well, because adjacent sides must be equal.
Kite – You can certainly have a kite, as the pairs of adjacent sides (radii) will always be equal.
Any hints would be truly appreciated; I feel like an idiot staring at this problem in Geometer's Sketchpad.