Quantum Circuit Confusion On Time Evolution

[thatboi]

Hi all,
When working in the Heisenberg picture, we can represent implementing time evolution on an operator via a Hamiltonian H through a quantum circuit type picture like the following:

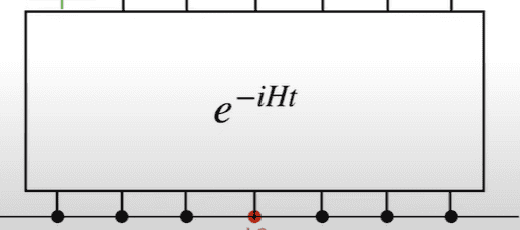
where time is on the vertical axis and increases going up and the block represents the unitary gate $e^{-iHt}$. However, I am struggling to picture how this would look on a circuit if instead, we wanted to conjugate some operator $O$ via the unitaries $e^{-iH_{1}t},e^{-iH_{2}t}$ where $[H_{1},H_{2}] \neq 0$. That is, $O(t) = e^{-iH_{2}t}e^{-iH_{1}t}Oe^{iH_{1}t}e^{iH_{2}t}$. Vertically stacking the gates on top of each other doesn't seem to make much sense to me since it would then seem to imply that we have elapsed a time $2t$ through this time evolution.
Any thoughts?

 

[Demystifier]

Is it really important how much time was spent? If not, then vertically stacking gates is OK. If yes, then you need to find an operator $H$ such that
$$e^{iH_1t}e^{iH_2t}=e^{iHt}$$
For that purpose, you need to use some version of Baker-Campbell-Hausdorff formula.