Gargi
- 5
- 0
- Homework Statement
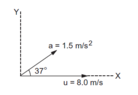
- A particle moves in the X-Y plane with a constant acceleration of 1.5 m/s^2 in the direction making an angle of 37° with the X-axis. At t = 0, the particle is at the origin and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t = 4.0 s. The graph corresponding to the question is attached herewith.
- Relevant Equations
- v = u + at.
v² = u² + 2as.
s = ut + ½at²
My initial approach to this question was breaking the components of acceleration in the x and y axes and applying the three equations of motion to find the final velocity as well as the final position. As we were expected to find the net final velocity of the particle, I found the resultant of the two components of final velocity in both the axes. This led to some complex solving of roots.
Alternate approach which went wrong: I broke the component of the initial velocity in the direction of the acceleration and find the final velocity in the direction of acceleration. The final velocity achieved using this did not match the right answer.
Please tell me what is wrong with my approach. Please tell me in the comments regarding any further requirements.
Alternate approach which went wrong: I broke the component of the initial velocity in the direction of the acceleration and find the final velocity in the direction of acceleration. The final velocity achieved using this did not match the right answer.
Please tell me what is wrong with my approach. Please tell me in the comments regarding any further requirements.