Question about length contraction and repulsive force

[Junhyoung Park]

If length contraction occurs due to relativistic effects, the atomic spacing becomes shorter. This should also increase the repulsive force between atoms. Then how can the stable bonding length remain short in such a scenario?

 

[PeroK]

If length contraction occurs due to relativistic effects, the atomic spacing becomes shorter. This should also increase the repulsive force between atoms. Then how can the stable bonding length remain short in such a scenario?

Length contraction is a coordinate effect. A body remains at rest in its own rest frame. If you fly past an object at half the speed of light, then the object cannot physically change on account of your motion relative to it.

 

[Ibix]

Then how can the stable bonding length remain short in such a scenario?

If you transform from the rest frame to a moving frame you must transform the fields and charges into that frame as well if you want to understand it. Nuclei and electrons are moving in the frame where the object is length contracted, so you will have currents and magnetic fields on the atomic scale. You'll also need relativistic quantum field theory to describe this accurately.

 

[pervect]

The A level answer to this question is easier to describe than the I level. Covariant formulations of electromagnetism exist, whereby all the tensor entities that describe the electromagnetic field transform via the Lorentz transform as appropriate to the number and placement of their indices.

These transformation laws guarantee that anything that's invariant stays invariant regardless of the coordinate choices (such as frame of reference in special relativity. It also can handle the curved space-times of GR, and other coordinate systems like polar coordinates).

It's possible to fixate on non-invariant quantities in electromagnetism , but it's more useful and productive to focus on things that are invariants. In this example, proper length would be an example of such an invariant - the frame-dependent length isn't an invariant, but the proper length is.

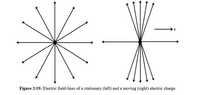
The I level answer has a lot more fiddly details. I really only recall the highlights. The electric field of a moving charge is NOT spherical. If you draw the field lines, the transverse fields are larger (you can tell the strength of the field from a field line diagram by how close the field lines are to each other - the closer they are, the higher the force). The longitudinal fields are weakened.

For an I level treatment google finds https://farside.ph.utexas.edu/teaching/355/Surveyhtml/node157.html. This includes the correct transformation laws between frames, and some diagrams of the field lines.

An image of the electric field lines of a moving charge gives some insight, if you are familiar enough with the field line formation to turn them into forces. I'll attach a copy of the relevant diagram from this site in an attachment for motivational purposes, I believe that is "fair use".

I'll add Google AI's summary of the field line rules here as well:

The key rules for field lines are: they always originate from a positive charge and end on a negative charge, they never cross each other, and the density of field lines represents the strength of the field, with more lines indicating a stronger field; essentially, the number of lines leaving a positive charge or approaching a negative charge is proportional to the magnitude of that charge.

So you can see the increase in the transverse field in this diagram because the field lines are more dense in the moving frame than the stationary - you can see the decrease in the longitudinal field because the field lines are less dense. If you want the more exact transformation rules, the website I linked to gives the equations.