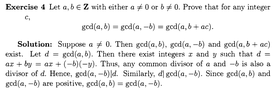Question about problem involving gcd

  • Context: MHB 
  • Thread starter Thread starter issacnewton
  • Start date Start date
  • Tags Tags
    Gcd
Click For Summary
SUMMARY

The discussion centers on the mathematical property that if \( d = \gcd(a, b) \), then it follows that \( d | \gcd(a, -b) \). This conclusion is derived from the fundamental definition of the greatest common divisor (gcd), which remains unchanged when one of the arguments is negated. Participants confirm this property as a standard result in number theory, emphasizing its importance in understanding gcd relationships.

PREREQUISITES
  • Understanding of the greatest common divisor (gcd)
  • Basic knowledge of number theory
  • Familiarity with mathematical notation and properties
  • Concept of divisibility in integers
NEXT STEPS
  • Study the properties of gcd in detail, including proofs and examples
  • Explore the Euclidean algorithm for calculating gcd
  • Learn about the implications of gcd in modular arithmetic
  • Investigate applications of gcd in solving Diophantine equations
USEFUL FOR

Students of mathematics, educators teaching number theory, and anyone interested in the properties of divisibility and gcd in integer arithmetic.

issacnewton
Messages
1,035
Reaction score
37
HelloI am studying the problem given in the attachement. In the solution given, it says "Similarly \( d|\gcd(a,-b) \) ". I could not understand why this is so.thanks
 

Attachments

  • 1.png
    1.png
    16.9 KB · Views: 124
Physics news on Phys.org
IssacNewton said:
HelloI am studying the problem given in the attachement. In the solution given, it says "Similarly \( d|\gcd(a,-b) \) ". I could not understand why this is so.thanks
$d|\gcd(a,-b)$ follows from the fact that $d=\gcd(a,b)$.
 
thanks...I should have realized that...
 

Similar threads

Undergrad Clarifications needed for an exercise in Hungerford's abstract algebra
  • · Replies 23 ·
Replies
23
Views
1K
Undergrad Understanding the Results of gcd(x,n)
  • · Replies 8 ·
Replies
8
Views
2K
MHB Prove that CnXCm isomorphic to Cgcd(m,n)XClcm(m,n)
  • · Replies 3 ·
Replies
3
Views
3K
MHB Properties of gcd's and relatively prime integers
  • · Replies 2 ·
Replies
2
Views
2K
MHB Does Z[root(-3)] Qualify as a GCD Domain?
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Questions about non existence of GCDs vs (coimages, cokernels)
  • · Replies 12 ·
Replies
12
Views
740
MHB How Do GCDs Coincide in Principal Ideals According to Rotman's Proposition 3.41?
  • · Replies 1 ·
Replies
1
Views
1K
MHB Are GCDs Always Defined in Integral Domains?
  • · Replies 2 ·
Replies
2
Views
2K
MHB GCDs of Polynomials: Reading Rotman's Corollary 3.58
  • · Replies 1 ·
Replies
1
Views
1K
MHB Greatest common divisor of a and b
  • · Replies 8 ·
Replies
8
Views
3K