Discussion Overview
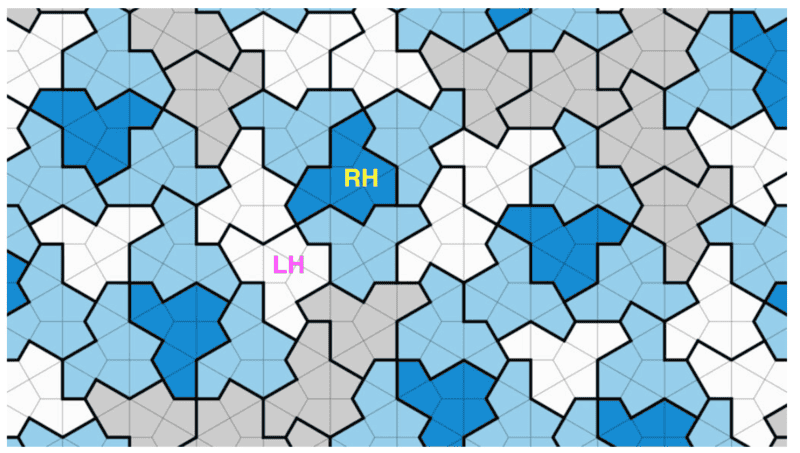
The discussion centers around the "Hat" tiling problem, specifically whether the shapes involved can be considered a single shape given that some are mirror images of others. Participants explore the implications of transformations allowed in tiling, including flipping and rotation, and whether these affect the classification of the shapes. The conversation touches on theoretical aspects of tiling, including aperiodicity and the constraints of different tiling groups.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
Main Points Raised
- Some participants question whether it is fair to consider the "Hat" tiling as a single shape due to the presence of mirror images.
- There is a discussion about the rules governing transformations in tiling, with some arguing that flipping is a valid transformation while others contend that certain classes of tiling do not permit it.
- One participant references a follow-up paper that addresses the question of whether a true single shape exists without mirror imaging.
- Another participant asserts that a true single shape without mirror imaging has been proven impossible, citing Bhattacharya's and Tao's work.
- Confusion arises regarding the claims made in an article about the "specters" from the arXiv paper, which some believe contradict the established proofs regarding tiling without reflections.
- Participants discuss the importance of definitions and constraints in classifying tiling problems, emphasizing that the inclusion of flipping may depend on the specific group of tilings being studied.
Areas of Agreement / Disagreement
Participants express differing views on the validity of flipping as a transformation in tiling, and whether the "Hat" tiling can be classified as a single shape. There is no consensus on the implications of the existing proofs regarding the existence of a true single shape without mirror imaging, as some participants reference conflicting interpretations of recent literature.
Contextual Notes
Limitations in the discussion include the dependence on definitions of nonperiodicity and the specifications of what qualifies as tiles. The conversation also highlights unresolved mathematical steps regarding the classification of tilings and the implications of transformations.