Question on delta potential function

[Brown Arrow]

NOT A HOME WORK QUESTION

how do i know if a delta potential function is given if its solution is even or odd? do i look for symettry or something

take this function for example:

V(x)= -alpha[delta(x+a) + delta(xa)]

i skeched the following graph.

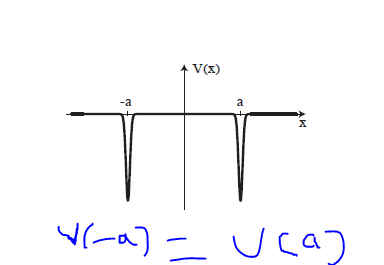
since V(-a)=V(a)...

 

[nonequilibrium]

Well, V(-a) = V(a) is the definition of an even function, so it's even. Graphically, this means the graph is symmetric around the y-axis, which is also the case.

Uneven functions: V(-a) = -V(a) & the graph is symmetric around the origin (like the sine function)

 

[Brown Arrow]

so we expect the solution to be even?

 

[Brown Arrow]

i just figured out that all delta function have both odd and even solution correct?...but how do we know that if it only has even or odd solution

 

[The_Duck]

For any even potential, you can argue that each energy eigenstate must be even or odd:

(1)If the potential is even, and psi(x) is an energy eigenstate, show that psi(-x) is an energy eigenstate with the same energy.
(2)Since there is no degeneracy of energy levels in one dimension, argue that psi(x) and psi(-x) must be linearly dependent
(3)Argue that the two possibilities are psi(x) = psi(-x) [an even solution] or psi(x) = -psi(-x) [an odd solution].

 

[Brown Arrow]

i can understand some of what your saying but not all b/c the course I am takeing is intro to modern physic... we don't talk interms of eigen

 

[seto6]

think of it like this...for even bound state there is a theorem alled the alternathing theorem. it states that if a function is even then you can do it seperately likr look for even then odd solution... there is no just even or odd solution...remember this is for even bounded ...function

hope this helps..

 

[Vanadium 50]

How many bound states does a single delta function have? How many do two have? Can you draw their wavefunctions?

 

[Brown Arrow]

only one bound state is possible no?

 

[K^2]

Depending on the strength of these delta functions, you can have two solutions, even and odd. They are both valid solutions, but even solution has lower energy. You can usually tell that without solving the equation by the fact that odd solution has a node, and these generally have higher energy.

Best thing to do is just go ahead and solve the problem. You'll then see at which strengths you have two solutions, just the even solution, or no solutions.