Discussion Overview
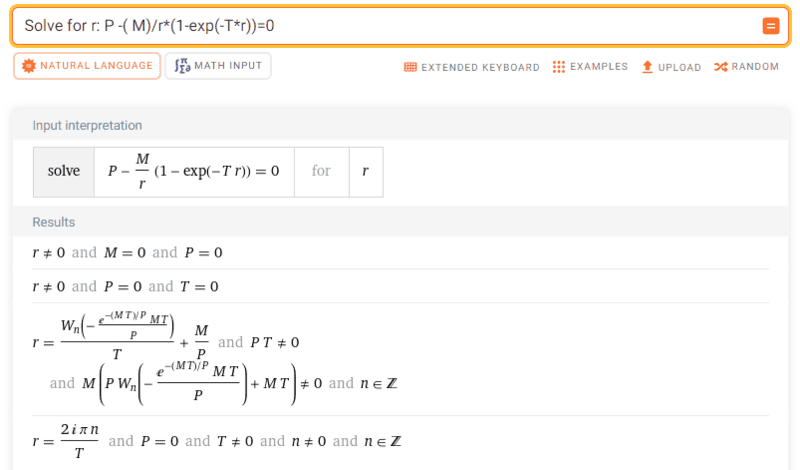
The discussion revolves around the differences between the Lambert W function and its branches, particularly ##W_n(x)##, in the context of solving equations involving exponential terms. Participants explore the application of the Lambert W function to manipulate equations and derive solutions, while also addressing the concept of analytic continuation and its implications.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants question the difference between the standard Lambert W function ##W(x)## and its branches ##W_n(x)##, particularly in the context of specific equations.
- There is mention of the analytic continuation of the product log function, with some participants seeking clarification on what this entails and how it differs from the standard Lambert W function.
- One participant suggests that ##W_0## is applicable under certain conditions related to the argument of the function, specifically when $$\frac{-MT}{P} \times e^{\frac{-MT}{P}} \geq -e^{-1}$$.
- Another participant attempts to work backwards from a given solution, expressing confusion about missing steps in their manipulation of the equation.
- There is a proposal to make a variable substitution to simplify the original equation, leading to a solution involving the Lambert W function.
- Participants discuss the practical implications of the value of ##n## in the context of real-world applications, suggesting that ##n=0## is often a reasonable assumption.
Areas of Agreement / Disagreement
Participants express varying levels of understanding regarding the Lambert W function and its branches, with some agreeing on the need for further clarification on analytic continuation, while others present different approaches to solving related equations. The discussion remains unresolved regarding the exact implications of the differences between ##W(x)## and ##W_n(x)##.
Contextual Notes
Participants acknowledge the complexity of the topic, particularly in relation to analytic continuation and the conditions under which different branches of the Lambert W function are used. There are references to specific mathematical manipulations and conditions that have not been fully resolved.
Who May Find This Useful
This discussion may be useful for individuals interested in advanced mathematics, particularly those exploring the Lambert W function, its applications in solving equations, and the concept of analytic continuation in complex analysis.