Discussion Overview
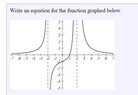
The discussion revolves around writing equations for rational functions based on provided graphs. Participants are attempting to derive the equations from the characteristics of the graphs, including zeros, asymptotes, and intercepts. The scope includes mathematical reasoning and problem-solving related to pre-calculus concepts.
Discussion Character
- Mathematical reasoning
- Homework-related
- Technical explanation
Main Points Raised
- One participant identifies a zero at $x=1$, a y-intercept at $(0,-1)$, and vertical asymptotes at $x=\pm2$, proposing a function form involving constants $a$ and $b$.
- Another participant suggests that the zero at $x=1$ has even multiplicity, indicating the numerator should be $(x-1)^2$, and notes vertical asymptotes at $x=\pm3$.
- There is uncertainty regarding the horizontal asymptote, with one participant stating that the degree of the numerator must be less than that of the denominator.
- One participant proposes a function form $f(x) = \dfrac{a(x-1)^2}{b(x+3)(x-3)^2}$, indicating that the factor $(x-3)$ in the denominator is squared based on the function's behavior near the vertical asymptote.
- Participants express difficulty in determining the correct values for constants $a$ and $b$, with one suggesting $a=1$ and calculating $b$ based on a specific point on the graph.
Areas of Agreement / Disagreement
Participants generally agree on the presence of certain features in the graphs, such as zeros and asymptotes. However, there is disagreement and uncertainty regarding the exact forms of the equations and the behavior of the functions, particularly concerning the horizontal asymptote and the multiplicity of factors.
Contextual Notes
Participants note the lack of additional points on the graphs to definitively determine the constants $a$ and $b$, which complicates the formulation of the equations.
