scakpinar
- 2
- 2
- TL;DR
- I am confused about why event horizons and the time direction cannot be observer dependent near black holes.
Hello everyone,
I have no formal training in theoretical physics or advanced mathematics. I have been trying to build intuition about general relativity, especially black holes and event horizons, by reading popular and semi-technical sources.
While reading that time and space effectively exchange roles inside a black hole, I tried to form an intuitive picture of how this can be understood physically. In the process, I found myself considering a way of thinking in which the accessibility of events near the horizon seems to depend on the observer’s position and motion.
My intuition keeps getting stuck on the following point: as different observers use different local frames, the same position-time graph of a light ray appears differently when projected onto their local coordinates. This line of thinking also seemed to account for effects such as the apparent ‘freezing’ of light near a black hole, or the way its coordinate speed can appear to approach zero for a distant observer. In the same way, it appeared to offer an intuitive explanation for why infalling objects seem to take an infinite time to cross the event horizon when viewed from afar. Within this picture, the fact that light cannot escape from the event horizon also seemed to be related to its coordinate velocity approaching zero relative to the observer. This makes it tempting to think that what counts as “beyond the horizon” might appear different to different observers even though chatgpt says the global event horizon is defined in an observer-independent way. It also seems to suggest that light and observers moving forward in time in their own local frames may, due to gravitational effects, have their time direction appear to tilt in an increasingly distorted manner to a different direction and eventually possibly backward when described from the perspective of a distant observer.
This analogy also helps me intuitively grasp gravitational time dilation without using mathematics, as well as why an object ‘entering’ a black hole event horizon—where even light cannot escape—does not experience or notice passing through any special region at the moment of crossing.
Honestly, I cannot see where this intuition must fail. I tried to argue this point with ChatGPT, but I could not get a satisfying explanation of *why* this picture cannot work, only that it does not.
Could someone explain, at a conceptual or minimal-math level, where this intuition breaks down? In particular, why can the event horizon not be observer-relative, and why can the time direction not tilt in the way suggested by this intuition?
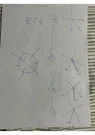
If it helps, I am attaching a photo of a diagram illustrating this intuition. Thank you for your patience.
I have no formal training in theoretical physics or advanced mathematics. I have been trying to build intuition about general relativity, especially black holes and event horizons, by reading popular and semi-technical sources.
While reading that time and space effectively exchange roles inside a black hole, I tried to form an intuitive picture of how this can be understood physically. In the process, I found myself considering a way of thinking in which the accessibility of events near the horizon seems to depend on the observer’s position and motion.
My intuition keeps getting stuck on the following point: as different observers use different local frames, the same position-time graph of a light ray appears differently when projected onto their local coordinates. This line of thinking also seemed to account for effects such as the apparent ‘freezing’ of light near a black hole, or the way its coordinate speed can appear to approach zero for a distant observer. In the same way, it appeared to offer an intuitive explanation for why infalling objects seem to take an infinite time to cross the event horizon when viewed from afar. Within this picture, the fact that light cannot escape from the event horizon also seemed to be related to its coordinate velocity approaching zero relative to the observer. This makes it tempting to think that what counts as “beyond the horizon” might appear different to different observers even though chatgpt says the global event horizon is defined in an observer-independent way. It also seems to suggest that light and observers moving forward in time in their own local frames may, due to gravitational effects, have their time direction appear to tilt in an increasingly distorted manner to a different direction and eventually possibly backward when described from the perspective of a distant observer.
This analogy also helps me intuitively grasp gravitational time dilation without using mathematics, as well as why an object ‘entering’ a black hole event horizon—where even light cannot escape—does not experience or notice passing through any special region at the moment of crossing.
Honestly, I cannot see where this intuition must fail. I tried to argue this point with ChatGPT, but I could not get a satisfying explanation of *why* this picture cannot work, only that it does not.
Could someone explain, at a conceptual or minimal-math level, where this intuition breaks down? In particular, why can the event horizon not be observer-relative, and why can the time direction not tilt in the way suggested by this intuition?
If it helps, I am attaching a photo of a diagram illustrating this intuition. Thank you for your patience.