Rewriting the Toeplitz Conjecture

[MevsEinstein]

TL;DR

I was thinking of the Toeplitz conjecture in a backward motion. Maybe it makes proving it easier?

The Toeplitz Conjecture (better known as the inscribed square problem) states that all Jordan curves have an inscribed square. It has been stated in the early 1900's and remains an open problem.

I drew a square and then making a ton of curves that touch its four vertices:

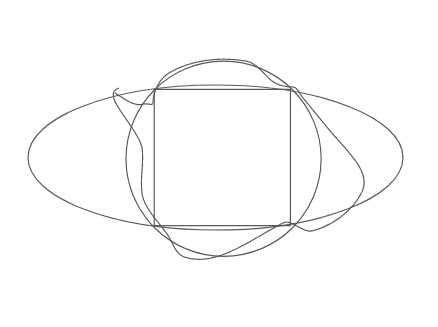
This shows that the square is inscribed in many curves.

Now what if I transformed (dilate, translate, rotate, or reflect) these curves? Well, those curves will also have inscribed squares. From this diagram, I rephrased the Toeplitz conjecture as such: When we make every possible transform on all the curves that have the square above as an inscribed square, they will map on to every other Jordan curve.

So I was thinking, does this make the Toeplitz conjecture easier to prove? I thought that my definition can help with using set notation.

 

[fresh_42]

It is the other way around: Given any closed Jordan curve, is there always an inscribed square?

(copyright by Claudio Rocchini, Wikipedia, https://de.wikipedia.org/wiki/Toeplitz-Vermutung)

The black Jordan curve has many inscribed (= contains all 4 vertices) squares.

The already proven special cases (convex, piecewise smooth) make it hard to draw other examples. Plus the fact that it is still open after more than a century.

 

[mathwonk]

mevseinstein, note that your drawings are of the case of a strongly inscribed square, more restrictive than the ones meant in the conjecture, as explained by fresh42.

may i suggest you try warming up by attempting an easier case?, e.g. try to prove that a jordan curve always contains the vertices of some equilateral triangle. your Idea of using dilation and rotation are sufficient in this case, with some continuity arguments. or perhaps you already know how to do this.

 

[malawi_glenn]

Now what if I transformed (dilate, translate, rotate, or reflect) these curves?

I think that is only possible for "smooth" curves, and not for these "nowhere differentiable" curves (like fractal curves)

 

[WWGD]

It is the other way around: Given any closed Jordan curve, is there always an inscribed square?

View attachment 304723

(copyright by Claudio Rocchini, Wikipedia, https://de.wikipedia.org/wiki/Toeplitz-Vermutung)

The black Jordan curve has many inscribed (= contains all 4 vertices) squares.

The already proven special cases (convex, piecewise smooth) make it hard to draw other examples. Plus the fact that it is still open after more than a century.

Don't mean to nitpick, just to make sure we're using the same definitions:

A Jordan Curve is , in my understanding, close by definition; homeomorphic to the standard unit circle ( $x \in \mathbb R^2 : || x||=1$)

I guess not every choice of homeomorphism will take inscribed squares to inscribed squares.

 

[fresh_42]

Don't mean to nitpick, just to make sure we're using the same definitions:

A Jordan Curve is , in my understanding, close by definition; homeomorphic to the standard unit circle ( $x \in \mathbb R^2 : || x||=1$)

I guess not every choice of homeomorphism will take inscribed squares to inscribed squares.

I didn't look it up (and of course don't remember the correct definition anymore). I just read the Wikipedia article on Toeplitz and it said that the cases "piecewise smooth" and "convex" are proven. That led me to the assumption that Jordan is closed and possibly of genus 1.

 

[WWGD]

I didn't look it up (and of course don't remember the correct definition anymore). I just read the Wikipedia article on Toeplitz and it said that the cases "piecewise smooth" and "convex" are proven. That led me to the assumption that Jordan is closed and possibly of genus 1.

This seems to be leading to Algebraic Geometry. Maybe @mathwonk can clarify here? IIRC, genus 0 curves are those that are parametrizable? Or am I way off? Edit: I thought genus applies to higher dimensional objects, not to curves.

 

[fresh_42]

This seems to be leading to Algebraic Geometry. Maybe @mathwonk can clarify here? IIRC, genus 0 curves are those that are parametrizable? Or am I way off? Edit: I thought genus applies to higher dimensional objects, not to curves.

I don't care. I just wanted to say "without crossings" a bit more sophisticated. Now I look it up.

Jordan curve = continuous, injective image of [0,1].

This excludes crossings, but requires everything else to be mentioned: closed, rectifiable, 0-homotope, smooth, convex or whatever.