- #1
Vibhukanishk
- 2
- 0
What to say about this?
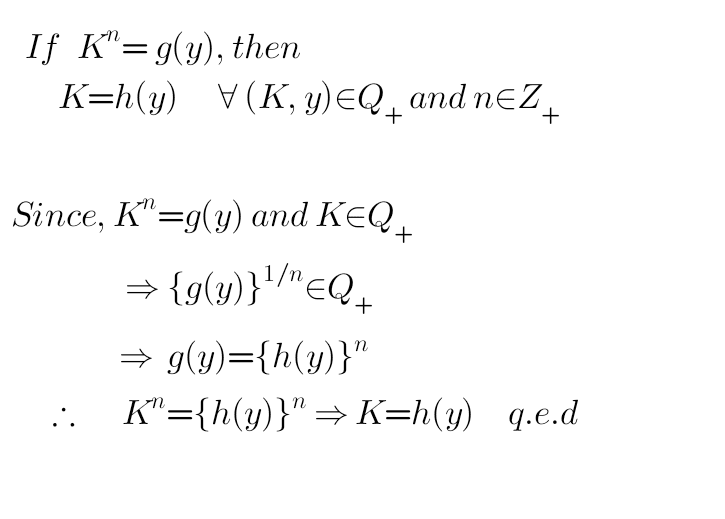
Is the logic used in the solution supports the statement?
Is the logic used in the solution supports the statement?
Rewriting this logic statement
- I
- Thread starter Vibhukanishk
- Start date
-
- Tags
- Logic
In summary, rewriting a logic statement is done to simplify, clarify, or provide a different perspective on the problem at hand. A statement may need to be rewritten if it is too complex, contains errors or contradictions, or can be expressed in a simpler way. The steps to rewriting a logic statement include identifying the main components, analyzing the logical structure, and simplifying or rephrasing it. Rewriting a logic statement can change its meaning, but the core logic should remain the same. If a statement is already correct, it may not be necessary to rewrite it, but it is helpful to review and revise for clarity and conciseness.
- #2
TeethWhitener
Science Advisor
Gold Member
- 2,618
- 2,228
No. You just asserted that ##g(y)=h(y)^n## with no justification.
- #3
- 18,994
- 23,995
There is quite a bit of information missing. E.g., there is no quantifier on ##h(y)## in the initial statement.
- #4
Vibhukanishk
- 2
- 0
TeethWhitener said:
- #5
TeethWhitener
Science Advisor
Gold Member
- 2,618
- 2,228
If you define ##g(y)## as ##h(y)^n##, then of course it's true, but there's also nothing to prove; it's all definitions.
1. What is the purpose of rewriting a logic statement?
Rewriting a logic statement is done to make it easier to understand and analyze. It can also help identify any errors or inconsistencies in the original statement.
2. When should a logic statement be rewritten?
A logic statement should be rewritten if it is too complex or difficult to understand, if it contains errors, or if it needs to be simplified for a specific purpose or audience.
3. What are some common methods for rewriting a logic statement?
Some common methods for rewriting a logic statement include breaking it down into smaller parts, using symbols and diagrams to represent concepts, and rephrasing it in simpler terms.
4. How can rewriting a logic statement improve its accuracy?
By rewriting a logic statement, errors or inconsistencies can be identified and corrected. It also allows for a more thorough analysis of the statement, leading to a more accurate representation of the logic being conveyed.
5. Are there any potential drawbacks to rewriting a logic statement?
One potential drawback is that the rewritten statement may lose some of its original meaning or nuance. It is important to carefully consider the purpose and audience when rewriting a logic statement to ensure its accuracy and effectiveness.
Similar threads
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics
-
Set Theory, Logic, Probability, Statistics