Narasoma
- 42
- 10
Everyone who is currently studying GR must be familiar with this picture. We find Riemann curvature by paraller transport a "test vector" around and see whether the vector changes its direction.
My question. How does it work with one dimensional Ring? A geomteric ring is intuitively curved but the only parallel transport possible for a vector to the point where it previously started, just give the sampe direction.
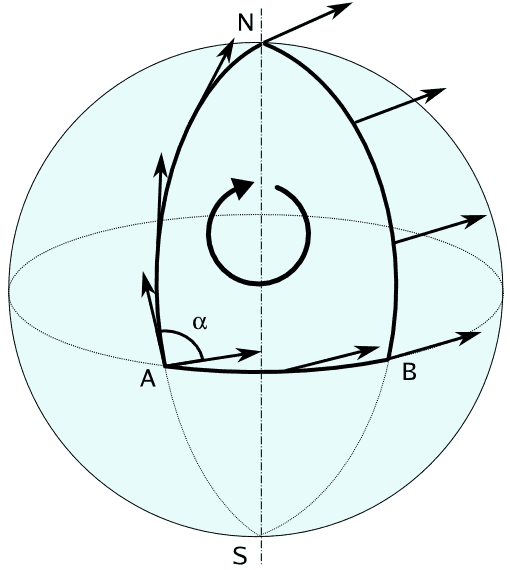
My question. How does it work with one dimensional Ring? A geomteric ring is intuitively curved but the only parallel transport possible for a vector to the point where it previously started, just give the sampe direction.