Tar
- 2
- 0
Hello,
I'm given the following exercise:
"A rod with neglected thickness exists. What is the relation between the α,β angles to Euler angles of orientation?
α is defined as the angle between the rod and its projection on the XY plane.
β is defined as the angle between the X-axis and the rod's projection on the XY plane.
(Note: We are using ZXZ Euler angles convention, having the following order of angles: ϕ,θ,ψ.)"
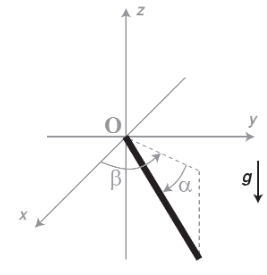
The answer is: α=θ+0.5π, β=ϕ
I don't understand why.
As far as I know, usually the body points in the e3 direction in the body frame. Initially the body frame points towards the original Z direction, after rotation of ϕ around the Z axis, and then rotation of θ around the x′ axis, we will receive the following:
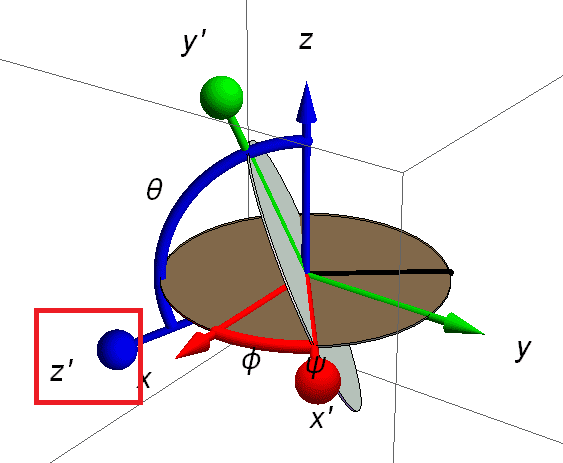
Note that the new z′ axis doesn't point to where it should be (according to the answer) and ϕ doesn't represent the angle between z' axis' projection on the XY plane and X-axis.
What am I missing?
Thank you.
Homework Statement
I'm given the following exercise:
"A rod with neglected thickness exists. What is the relation between the α,β angles to Euler angles of orientation?
α is defined as the angle between the rod and its projection on the XY plane.
β is defined as the angle between the X-axis and the rod's projection on the XY plane.
(Note: We are using ZXZ Euler angles convention, having the following order of angles: ϕ,θ,ψ.)"
The answer is: α=θ+0.5π, β=ϕ
I don't understand why.
The Attempt at a Solution
As far as I know, usually the body points in the e3 direction in the body frame. Initially the body frame points towards the original Z direction, after rotation of ϕ around the Z axis, and then rotation of θ around the x′ axis, we will receive the following:
Note that the new z′ axis doesn't point to where it should be (according to the answer) and ϕ doesn't represent the angle between z' axis' projection on the XY plane and X-axis.
What am I missing?
Thank you.
