maistral
- 235
- 17
Hello.
How do I solve this equation without killing the k(y) term:
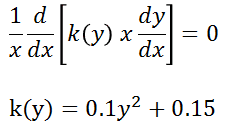
I managed to derive an analytical solution for this one. I intend to run the numerical solution via Runge-Kutta but I can't stop myself from killing the k(y) term. I'm starting to think I'm doing something wrong... It goes something like this:
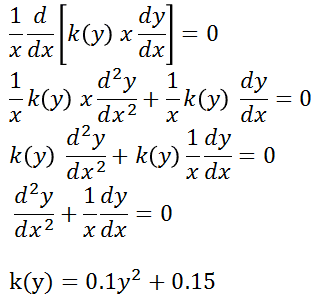
Even if I try and keep the k(y) term until I derive the systems of equations required to run Runge-Kutta, the integrator would then numerically kill it anyway. What should I do?
Any help please?
How do I solve this equation without killing the k(y) term:
I managed to derive an analytical solution for this one. I intend to run the numerical solution via Runge-Kutta but I can't stop myself from killing the k(y) term. I'm starting to think I'm doing something wrong... It goes something like this:
Even if I try and keep the k(y) term until I derive the systems of equations required to run Runge-Kutta, the integrator would then numerically kill it anyway. What should I do?
Any help please?