Discussion Overview
The discussion revolves around the relationship between the root mean square (RMS) and the Pythagorean theorem, exploring its geometric implications and potential applications in higher dimensions. Participants examine the mathematical connections and seek to understand the significance of these relationships in various contexts, including standard deviation.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
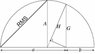
- One participant proposes that the RMS of the legs of a right triangle is equal to the leg of a square with the hypotenuse as its diagonal, suggesting a geometric interpretation.
- Another participant provides a modified figure to illustrate the geometric meaning of the RMS in relation to the Pythagorean theorem.
- A challenge is raised regarding the lengths in the figure, with a participant questioning the accuracy of the RMS length compared to the diagonal of a square and the arithmetic mean.
- A participant elaborates on the relationship between the RMS and the legs of a 45-45-90 triangle, suggesting that the RMS can be used to find average vector components and speculating on its broader implications.
- There is a query about the connection between standard deviation and the RMS, with a participant seeking clarification on whether deviations can be visualized in a similar geometric manner.
- A link to a Wikipedia article is shared, which discusses the geometric interpretation of standard deviation, indicating a perceived similarity to the RMS discussion.
Areas of Agreement / Disagreement
Participants express varying interpretations of the relationship between RMS and the Pythagorean theorem, with some agreeing on the geometric connection while others challenge specific mathematical claims. The discussion remains unresolved regarding the accuracy of the figures and the broader implications of these relationships.
Contextual Notes
There are unresolved mathematical steps and assumptions regarding the lengths and relationships discussed, particularly in the context of the figures and the application of RMS in higher dimensions.