Roark's Equations for Discontinuity Stresses Syntax

Click For Summary
SUMMARY

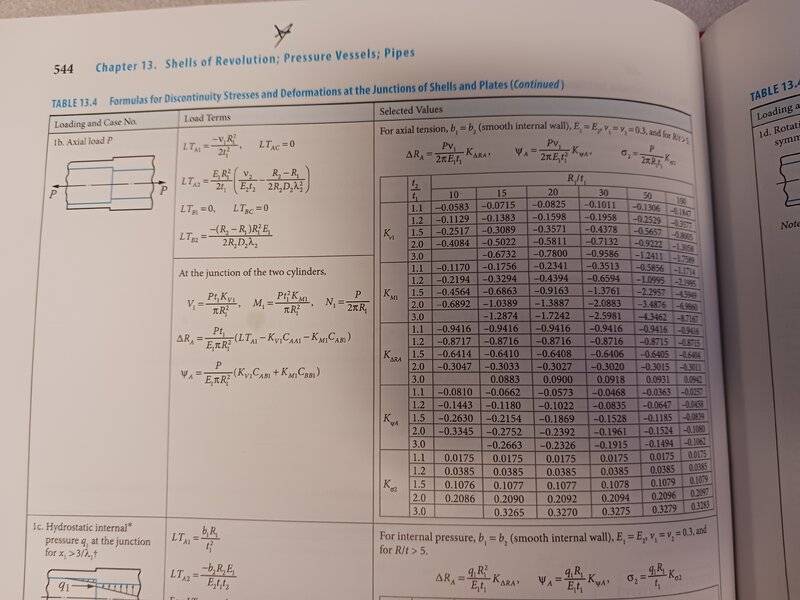
The discussion clarifies the meaning of R_A in Roark's Formulas for Stress and Strain 9E, specifically in Table 13.4 on page 543. R_A is defined as the radius of common circumference, representing the intersection of the midsurfaces of two different shells, rather than any shared radius. When the left section is not curved, R_A equals R_1; however, if it is more circular, R_A is calculated as R_1 multiplied by the sine of the angle, measured vertically. It is important to note that R_A should not be confused with delta R_A, which appears in the referenced table.

PREREQUISITES
  • Understanding of Roark's Formulas for Stress and Strain 9E
  • Familiarity with stress analysis concepts
  • Knowledge of cylindrical shell theory
  • Basic trigonometry for calculating R_A
NEXT STEPS
  • Review Roark's Formulas for Stress and Strain 9E, focusing on Table 13.4
  • Study cylindrical shell theory and its applications in engineering
  • Learn about the calculation of intersection points in structural analysis
  • Explore advanced stress analysis techniques for composite materials
USEFUL FOR

Engineers, particularly those specializing in structural analysis and materials science, will benefit from this discussion, as well as students studying mechanical engineering principles related to stress and strain in cylindrical structures.

josep233
Messages
1
Reaction score
0
I am looking for clarification of some terms found in Roark's Formulas for Stress and Strain 9E. Table 13.4 pg 543 as well as preceding tables frequently reference R_A as the radius of common circumference. I take this to mean that this value could include any radius that both cylinders share through their thicknesses, but do not know for sure. To further confuse this, some tables say R_A = R_1. Does anyone with more exposure to this understand what R_A means?
20230524_111329.jpg
 
Last edited by a moderator:
Engineering news on Phys.org
R_A =radius of common circumference, i.e. it is defined as the intersection of the midsurfaces of the two different shells (not just any shared radius). It is generally defined as a vertical distance from an axis bisecting the shell horizontally. So if the left-most section isn't curved, then R_a should equal R_1.
1686676572241.png


If the left section is e.g. more circular, then the R_a is a function of R_1*sin() -> since R_a is measured vertically in the fashion the diagrams are usually portrayed, not radially.
1686676452828.png

It's maybe worth saying that R_A is not delta R_A, which is all I see in the table you shared.
 
Reply
  • Informative
Likes   Reactions: Tom.G

Similar threads

Roark's formulas for stress and strain
  • · Replies 2 ·
Replies
2
Views
25K
Stress/strain+general bending equation
  • · Replies 3 ·
Replies
3
Views
3K