Rounding error making my graphics barely off?

[SlurrerOfSpeech]

I'm trying to draw a circle and a (possibly rotated) square on a grid. I have the circle part down and it's the square that is giving me trouble. I am originally given 2 points which represent the coordinates containing opposite ends of the square. For example, those 2 points would be (8,14) and (16,14) in the following image.

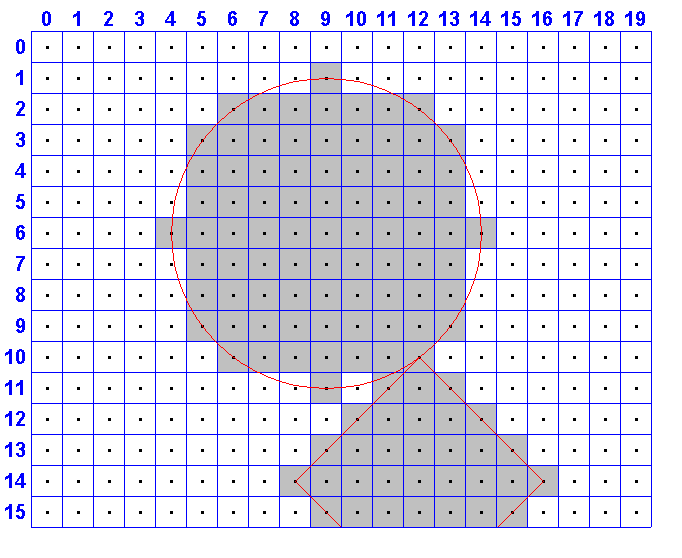and the output would look like

I had to rehash my memory of matrices, lines on graphs, etc., but eventually (after almost 10 hours) I came up with

    public void DrawSquare(double x1, double y1, double x3, double y3)
    {
        // Increment input coordinates so that they now are
        // at the center of the squares
        x1 += 0.5;
        y1 += 0.5;
        x3 += 0.5;
        y3 += 0.5;        // Ensure x1 <= x3
        if(x1 > x3)
        {
            SwapDoubles(ref x1, ref x3);
            SwapDoubles(ref y1, ref y3);
        }

        // Get midpoints of x-y pairs
        double midx = (x1 + x3) / 2;
        double midy = (y1 + y3) / 2;
      
        // Get the slope of the line y = mx + b that goes through the two points
        double ydiff = y3 - y1;
        double xdiff = x3 - x1;
        double m = (xdiff == 0 || ydiff == 0) ? 0 : ydiff / xdiff;

        // Get the slopes of the above line rotated -45 deg and 45 deg
        double m1 = RotateSlope(m, Math.PI / 4);
        double m2 = RotateSlope(m, -1 * Math.PI / 4);
        // Get the intercepts for the lines with the above slopes passing through the midpoint
        double b1 = midy - m1 * midx;
        double b2 = midy - m2 * midx;

        // now we have two lines y = m1 * x + b1 and y = m2 * x + b2 which are at 45 degree
        // angles from the line y = mx + b passing through the two original points, and
        // which pass through the midpoint of the original two points

        // Get distance from center to lines that run across the sides of the square
        double dist = Math.Sqrt(Math.Pow((double)x1 - midx, 2) + Math.Pow((double)y1 - midy, 2)) / Math.Sqrt(2);

        DrawInRange((Coordinate<int> coord) =>
        {
            // distance from middle of coordinate to line 1
            double d1 = ClosestDistanceToLine(m1, -1, b1, coord.X + 0.5, coord.Y + 0.5);
            // distance from middle coordinate to line 2
            double d2 = ClosestDistanceToLine(m2, -1, b2, coord.X + 0.5, coord.Y + 0.5);
            return  d1 <= dist && d2 <= dist;
        });
    }

    // https://en.wikipedia.org/wiki/Rotation_matrix
    static double RotateSlope(double m, double angle)
    {
        double y = m;
        double x = 1;
        double _x = Math.Cos(angle) * x + Math.Sin(angle) * y;
        double _y = -1 * Math.Sin(angle) * x + Math.Cos(angle) * y;
        return _y / _x;
    }

    // finds the closest distance beteen the line y = mx + b and the point (x0, y0)
    // http://www.intmath.com/plane-analytic-geometry/perpendicular-distance-point-line.php
    static double ClosestDistanceToLine(double A, double B, double C, double x0, double y0)
    {
        double numerator = Math.Abs(A * x0 + B * y0 + C);
        double denominator = Math.Sqrt(Math.Pow(A, 2.0) + Math.Pow(B, 2.0));
        return  numerator / denominator;
    }

which is giving me output slightly off

Any idea why?

Full code dump if you want:

using System;
using System.Collections.Generic;
using System.Linq;

class Coordinate<T>
{
    public T X { get; private set; }
    public T Y { get; private set; }

    public Coordinate(T x, T y)
    {
        X = x;
        Y = y;
    }
}

class RasterGraphics
{
    public int Width { get; private set; }
    public int Height { get; private set; }
    public char[,] Graph { get; private set; }

    public RasterGraphics(int width, int height)
    {
        Width = width;
        Height = height;
        Graph = new char[height, width];
        for(int i = 0; i < height; ++i)
            for(int j = 0; j < width; ++j)
                Graph[i, j] = '.';
    }

    public void DrawCircle(int x, int y, int radius)
    {
        double dx = (double)x + 0.5, dy = (double)y + 0.5;
        DrawInRange((Coordinate<int> coord) =>
        {
            Coordinate<double> center = new Coordinate<double>((double)coord.X + 0.5, (double)coord.Y + 0.5);
            double dist = Math.Sqrt(Math.Pow(dx - center.X, 2.0) + Math.Pow(dy - center.Y, 2.0));
            return dist <= radius;
        });
    }

    public void DrawInRange(Func<Coordinate<int>,bool> condition)
    {
        IEnumerable<Coordinate<int>> coordsInRange = GetCoords().Where(condition);
        foreach(Coordinate<int> coord in coordsInRange)
            Graph[coord.Y, coord.X] = '#';
    }

    private IEnumerable<Coordinate<int>> GetCoords()
    {
        for(int i = 0, m = Graph.GetLength(0); i < m; ++i)
            for(int j = 0, n = Graph.GetLength(1); j < n; ++j)
                yield return new Coordinate<int>(j, i);
    }

    private static void SwapDoubles(ref double i, ref double j)
    {
        double temp = i;
        i = j;
        j = temp;
    }

    public void DrawSquare(double x1, double y1, double x3, double y3)
    {
        // Increment input coordinates so that they now are
        // at the center of the squares
        x1 += 0.5;
        y1 += 0.5;
        x3 += 0.5;
        y3 += 0.5;        // Ensure x1 <= x3
        if(x1 > x3)
        {
            SwapDoubles(ref x1, ref x3);
            SwapDoubles(ref y1, ref y3);
        }

        // Get midpoints of x-y pairs
        double midx = (x1 + x3) / 2;
        double midy = (y1 + y3) / 2;
      
        // Get the slope of the line y = mx + b that goes through the two points
        double ydiff = y3 - y1;
        double xdiff = x3 - x1;
        double m = (xdiff == 0 || ydiff == 0) ? 0 : ydiff / xdiff;

        // Get the slopes of the above line rotated -45 deg and 45 deg
        double m1 = RotateSlope(m, Math.PI / 4);
        double m2 = RotateSlope(m, -1 * Math.PI / 4);
        // Get the intercepts for the lines with the above slopes passing through the midpoint
        double b1 = midy - m1 * midx;
        double b2 = midy - m2 * midx;

        // now we have two lines y = m1 * x + b1 and y = m2 * x + b2 which are at 45 degree
        // angles from the line y = mx + b passing through the two original points, and
        // which pass through the midpoint of the original two points

        // Get distance from center to lines that run across the sides of the square
        double dist = Math.Sqrt(Math.Pow((double)x1 - midx, 2) + Math.Pow((double)y1 - midy, 2)) / Math.Sqrt(2);

        DrawInRange((Coordinate<int> coord) =>
        {
            // distance from middle of coordinate to line 1
            double d1 = ClosestDistanceToLine(m1, -1, b1, coord.X + 0.5, coord.Y + 0.5);
            // distance from middle coordinate to line 2
            double d2 = ClosestDistanceToLine(m2, -1, b2, coord.X + 0.5, coord.Y + 0.5);
            return  d1 <= dist && d2 <= dist;
        });
    }

    // https://en.wikipedia.org/wiki/Rotation_matrix
    static double RotateSlope(double m, double angle)
    {
        double y = m;
        double x = 1;
        double _x = Math.Cos(angle) * x + Math.Sin(angle) * y;
        double _y = -1 * Math.Sin(angle) * x + Math.Cos(angle) * y;
        return _y / _x;
    }

    // finds the closest distance beteen the line y = mx + b and the point (x0, y0)
    // http://www.intmath.com/plane-analytic-geometry/perpendicular-distance-point-line.php
    static double ClosestDistanceToLine(double A, double B, double C, double x0, double y0)
    {
        double numerator = Math.Abs(A * x0 + B * y0 + C);
        double denominator = Math.Sqrt(Math.Pow(A, 2.0) + Math.Pow(B, 2.0));
        return  numerator / denominator;
    }

    public void Print()
    {
        for(int i = 0, m = Graph.GetLength(0); i < m; ++i)
            Console.WriteLine(GetRow(i));
    }

    private string GetRow(int row)
    {
        int n = Graph.GetLength(1);
        char[] letters = new char[n];
        for(int j = 0; j < n; ++j)
            letters[j] = Graph[row, j];
        return new string(letters);
    }
}

class Solution
{
    static void Main(String[] args)
    {
        int w = 20;
        int h = 16;
        int circleX = 9;
        int circleY = 6;
        int r = 5;
        int x1 = 16;
        int y1 = 14;
        int x3 = 8;
        int y3 = 16;
        var raster = new RasterGraphics(w, h);
        raster.DrawCircle(circleX, circleY, r);
        raster.DrawSquare(x1, y1, x3, y3);
        raster.Print();
    }
}

 

[mfb]

Did you check the intermediate results of your calculations? Is your angle right, are your calculated corners right, ...?

 

[newjerseyrunner]

I didn't read all of the code, but it looks like your square is off by a factor of 0.5 units.