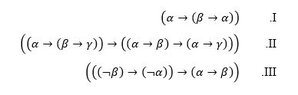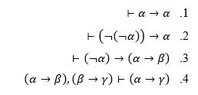Yankel
- 390
- 0
Hello to you all,
I am trying to prove the following:
\[\vdash \left ( p\rightarrow \left ( p\rightarrow q \right ) \right )\rightarrow \left ( p\rightarrow q \right )\]
I was given a table with the proof stages, and I had to fill the blanks. Sometimes the blanks were the rule or axiom used in this stage, and sometimes it was the result of using the rule/axiom. I filled all, but I can't figure out the last stage. More specifically, I can't figure out which rule / axiom was used in the last stage (stage 7). I have completed all other stages, and I think it's correct.
I am attaching as figures, the table of the proof, the 3 axioms I am allowed to use (I am using the L deductive system), and 4 statements which were proved already and can be used. In addition, the only inference rule is the modus ponens.
Thank you in advance for helping me complete the last stage.
View attachment 6043View attachment 6044View attachment 6045
I am trying to prove the following:
\[\vdash \left ( p\rightarrow \left ( p\rightarrow q \right ) \right )\rightarrow \left ( p\rightarrow q \right )\]
I was given a table with the proof stages, and I had to fill the blanks. Sometimes the blanks were the rule or axiom used in this stage, and sometimes it was the result of using the rule/axiom. I filled all, but I can't figure out the last stage. More specifically, I can't figure out which rule / axiom was used in the last stage (stage 7). I have completed all other stages, and I think it's correct.
I am attaching as figures, the table of the proof, the 3 axioms I am allowed to use (I am using the L deductive system), and 4 statements which were proved already and can be used. In addition, the only inference rule is the modus ponens.
Thank you in advance for helping me complete the last stage.
View attachment 6043View attachment 6044View attachment 6045