MHB Salim's question at Yahoo Answers regarding trigonometry and circular sectors

[MarkFL]

Here is the question:

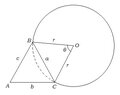
How to solve this maths problem?


So we have a triangle ABC with given sides. On the BC side, there's a part of a circle (we do not know how much of a circle). We are asked to find the angle A to ensure that the part of a circle has the same area as the triangle. The problem boils down to finding how to calculate the area of the part of circle. So how would you go about doing it?
Thanks

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Re: Salim's question at Yahoo! Answers regarding trignometry and circular sectors

Hello Salim,

Please refer to the following diagram:

View attachment 1805

We may determine $\theta$ using the Law of Cosines:

$$a^2=2r^2\left(1-\cos(\theta) \right)$$

$$\theta=\cos^{-1}\left(\frac{2r^2-a^2}{2r^2} \right)$$

From this, we may determine the area $A_S$ of circular sector $OBC$:

$$A_S=\frac{1}{2}r^2\theta=\frac{1}{2}r^2\cos^{-1}\left(\frac{2r^2-a^2}{2r^2} \right)$$

And we may now also determine the area $A_T$ of triangle $OBC$:

$$A_T=\frac{1}{2}r^2\sin(\theta)=\frac{1}{2}r^2\frac{a\sqrt{4r^2-a^2}}{2r^2}=\frac{a\sqrt{4r^2-a^2}}{4}$$

Thus the portion of the circle's area $A_O$ outside the triangle is:

$$A_O=\pi r^2-\frac{1}{2}r^2\cos^{-1}\left(\frac{2r^2-a^2}{2r^2} \right)+\frac{a\sqrt{4r^2-a^2}}{4}$$

Equating this to the area of triangle $ABC$, we obtain:

$$\frac{1}{2}bc\sin(A)=\pi r^2-\frac{1}{2}r^2\cos^{-1}\left(\frac{2r^2-a^2}{2r^2} \right)+\frac{a\sqrt{4r^2-a^2}}{4}$$

Hence, solving for $A$, we obtain:

$$A=\sin^{-1}\left(\frac{2r^2\left(2\pi-\cos^{-1}\left(\dfrac{2r^2-a^2}{2r^2} \right) \right)+a\sqrt{4r^2-a^2}}{2bc} \right)$$