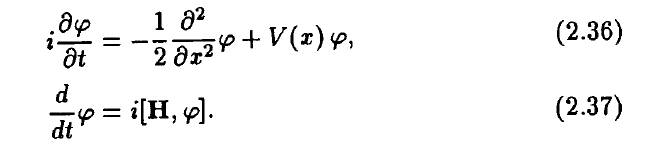Discussion Overview
The discussion centers around the relationship between the Schrödinger equation and the Heisenberg equation of motion within the context of quantum field theory. Participants are exploring the mathematical derivation and implications of these equations, particularly in relation to specific equations and notation from Hatfield's book.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant questions how to derive the Schrödinger equation from the Heisenberg equation of motion, expressing difficulty with an integral form of the Hamiltonian.
- Another participant suggests using a specific equation (2.54) and notes that the Hamiltonian is conserved in the Heisenberg picture, implying that the integral can be evaluated at any time.
- A different participant expresses confusion regarding the notation and the treatment of operators that are integrals, particularly in the context of commutation relations.
- One participant attempts to clarify their understanding by rewriting the commutation relation and manipulating the integrals, seeking confirmation on the correctness of their mathematical steps.
- Another participant provides a detailed explanation of the Hamiltonian's time independence and its implications for evaluating commutators, while also introducing a general formula for commutation relations involving multiple operators.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and familiarity with the notation and mathematical treatment involved. There is no clear consensus on the derivation process or the handling of specific integrals and operators, indicating ongoing debate and exploration of the topic.
Contextual Notes
Participants highlight potential confusion regarding the notation and the treatment of integrals in the context of quantum field theory. There are unresolved questions about the correct application of commutation relations and the implications of the Hamiltonian's time independence.