Heisenberg Definition and 309 Threads

Werner Karl Heisenberg (; German pronunciation: [ˈvɛɐ̯nɐ ˈhaɪzn̩ˌbɛɐ̯k] (listen); 5 December 1901 – 1 February 1976) was a German theoretical physicist and one of the key pioneers of quantum mechanics. He published his work in 1925 in a breakthrough paper. In the subsequent series of papers with Max Born and Pascual Jordan, during the same year, this matrix formulation of quantum mechanics was substantially elaborated. He is known for the uncertainty principle, which he published in 1927. Heisenberg was awarded the 1932 Nobel Prize in Physics "for the creation of quantum mechanics".Heisenberg also made important contributions to the theories of the hydrodynamics of turbulent flows, the atomic nucleus, ferromagnetism, cosmic rays, and subatomic particles. He was a principal scientist in the German nuclear weapons program during World War II. He was also instrumental in planning the first West German nuclear reactor at Karlsruhe, together with a research reactor in Munich, in 1957.
Following World War II, he was appointed director of the Kaiser Wilhelm Institute for Physics, which soon thereafter was renamed the Max Planck Institute for Physics. He was director of the institute until it was moved to Munich in 1958. He then became director of the Max Planck Institute for Physics and Astrophysics from 1960 to 1970.
Heisenberg was also president of the German Research Council, chairman of the Commission for Atomic Physics, chairman of the Nuclear Physics Working Group, and president of the Alexander von Humboldt Foundation.

View More On Wikipedia.org
Recent contents Top users
  1. S

    B Heisenberg's indeterminacy principle with non-point particles ?

    Hi. I was just wondering. Why does Heisenberg's principle of indeterminacy say that we can't know the position and velocity (momentum) of a particle with any precision, when a particle isn't point-like anyway? It's like the position of a car, it's arbitrary and all we can say about its...
  2. T

    I Heisenberg Equations of Motion for Electron in EM-field

    Consider the Heisenberg picture Hamiltonian $$H(t) = \int_{\textbf{r}}\psi^{\dagger}(\textbf{r},t)\frac{(-i\hbar\nabla+e\textbf{A})^{2}}{2m}\psi(\textbf{r},t)$$ where ##\psi(\textbf{r},t)## is a fermion field operator. To find the equations of motion that ##\psi,\psi^{\dagger}## obey. I would...
  3. H

    A Deriving the perturbative expansion from Hubbard to Heisenberg

    In the youtube lecture “electron interaction and the Hubbard model” at the time 2:23:00, we have the following self-consistent equation with energy appearing at both sides: $$(\hat P \hat H_0 \hat P+\hat P \hat H_1 \hat Q (E-\hat Q \hat H_0 \hat Q)^{-1} \hat Q \hat H_1 \hat P) |\phi...
  4. I

    A Monte Carlo simulation for the classical isotropic 3D Heisenberg model

    here is my attempt to implement using python import numpy as np import matplotlib.pyplot as plt def initialize_spins(L): """Initialize a random spin configuration with unit magnitudes.""" spins = np.random.normal(size=(L, L, L, 3)) magnitudes = np.linalg.norm(spins, axis=-1...
  5. T

    I How is the Schrodinger equation related to the Heisenberg equation?

    How is the Schrondinger equation related to the Heisenberg equation?
  6. T

    I Interpreting Unitary Time Evolution

    Hi all, This should be a simple question but it has been bothering me for a bit: Consider 2 Hamiltonian terms ##H_{1},H_{2}## that satisfy ##[H_{1},H_{2}] = 0##. Suppose we are working in the Heisenberg picture and we time evolve some operator ##A## according to ##A(t) =...
  7. LittleSchwinger

    A Decoherence in the Heisenberg Picture

    When I'm teaching Advanced QM, I like to include how to describe some processes in the Heisenberg picture (e.g. double slit) so that a student's thinking isn't overly attached to the "dynamics of the quantum state", but they can also understand effects involving operator evolution. This is a...
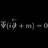
  8. qft-El

    A Heisenberg picture and Path integrals (Zee QFT)

    Reading the introduction to path integrals given in the latest edition of Zee's "Quantum field theory in a nutshell", I have found a remark which I don't really understand. The author is evaluating the free particle propagator ##K(q_f, t; q_i, 0)## $$\langle q_f\lvert e^{-iHt}\lvert q_i...
  9. Narasoma

    I The clarity of Heisenberg uncertainty

    We know from basic quantum mechanics that the Heisenberg uncertainty states that position and momentum can not be measured simultaneously with arbitrary precision. My question is, is this relation is due to the nature of the quantum system itself, or "merely" unbreachable limitation to our...
  10. D

    I Does Heisenberg Have Ontological Commitments to Quantum Theory?

    Heisenberg is regarded as a major figure of the Copenhagen interpretation. In a certain degree, he is influenced by Logical positivism. Despite of that, has he any ontological commitments regarding the Quantum theory? Or, he considers the Quantum theory merely as calculation procedure for...
  11. Bruno Cardin

    A Expectation value in Heisenberg picture: creation and annihilation

    So, I have a hamiltonian for screening effect, written like: $$ H=\sum_{k}^{}\epsilon_{k}c_{k}^{\dagger}c_{k}+ \frac{1}{\Omega}\sum_{k,q}^{}V(q,t)c_{k+q}^{\dagger}c_{k} $$ And I have to find an equation for the time evolution of the expected value of the operator ##c_{k-Q}^{\dagger}c_{k}##. I...
  12. L

    A SO(3) group, Heisenberg Hamiltonian

    We have commutation relation ##[J_j,J_k]=i \epsilon_{jkl}J_l## satisfied for ##2x2##, ##3x3##, ##4x4## matrices. Are in all dimensions these matrices generate ##SO(3)## group? I am confused because I think that maybe for ##4x4## matrices they will generate ##SO(4)## group. For instance for...
  13. M

    I Heisenberg Uncertainty Principle Violation?

    Hello, 2 questions please about the Uncertainty Principle and the following scenario: I shoot at each other, 2 electrons each with equal but opposite velocity such that they repel each other? (To me, this indicates that you know the momentum of each electron and you know each position...
  14. A. Neumaier

    I Heisenberg on ''uncertainty relation does not apply to the past''

    In post #30 of a now closed thread, vanhees71 wrote: The quote in question is from his 1930 book "The Physical Principles of the Quantum Theory" on p.20 of the English translation of the German original. There Heisenberg writes:
  15. H

    A Heisenberg lens and probabilities

    Hi Pf in her experiment Birgit Dopfer uses an https://www.researchgate.net/figure/color-online-The-Dopfer-experiment-of-the-Zeilinger-Group-Innsbruck-If-detector-D2-is_fig7_265787833 the distance between the source and the lens is 2f and the detector may be at the distance f or 2f behind the...
  16. Haorong Wu

    I Applying Heisenberg picture to density operator

    Suppose that a particle evolves from point A to point B. The state of the particle can be written as $$\rho=\sum \left | m\right >\rho_{mn}\left< n\right | .$$ Because the basis is evolving as the particle travels, I am considering applying the Heisenberg picture to the density operator. Let...
  17. L

    A Heisenberg equation of motion -- Partial derivative question

    Heisenberg equation of motion for operators are given by i\hbar\frac{d\hat{A}}{dt}=i\hbar\frac{\partial \hat{A}}{\partial t}+[\hat{A},\hat{H}]. Almost always ##\frac{\partial \hat{A}}{\partial t}=0##. When that is not the case?
  18. Jamister

    A Heisenberg Uncertainty Relation for mixed states

    How do you prove Heisenberg uncertainty relations for mixed states (density matrix), only from knowing the relation is true for pure states?
  19. K

    I Quantities in the Heisenberg Uncertainly Principle

    Hello, I am a Brazilian Physics student and would like to ask a question. Why are not all physical quantities related to each other by the degree of precision in the Heisenberg Uncertainty Principle? For example, why is it possible to determine the energy and position of a particle without its...
  20. Axel Togawa

    I Heisenberg Microscope: Exploring Single Photon Diffraction

    In the thought experiment proposed by Heisenberg, a single photon is scattered by the electron that we want to observe, and entering the microscope lens (the photon), it will create a diffraction pattern that gives the uncertainty on the position according to the law of optics. I wanted to ask...
  21. AndreasC

    I Pros and cons of Heisenberg and Schrodinger (and Feynman) pictures?

    So there's this professor who insists that the Heisenberg picture is all the rage and much superior in most ways to the Schrodinger picture. He compares it to how you don't use the Hamilton-Jacobi formulation of classical mechanics as much as the Hamiltonian one. Alright, I can buy it. I...
  22. LuisBabboni

    I Virtual particles and Heisenberg

    Hi people. Having as uncertainty principle that ΔE Δt≥ h/4Pi, why Δt≤ h/4PiΔE to allow the existence of a virtual particle? How ≥ becomes ≤ ? I think... real particles must obey ≥ so any particle that do not obey that is a virtual particle and thus why virtual particle needs to obey Δt≤...
  23. peguerosdc

    I Understanding the meaning of "uncertainty" in Heisenberg's UP

    Hi! I am checking Zettili's explanation on the uncertainty principle and I have this confusion on what the "uncertainty" really means which arises from the following statements: When introducing the uncertainty principle, for the case of position and momentum it states that: if the x-component...
  24. rad1um

    Stability of Classical Heisenberg Spins (Equation of Motion)

    Consider the classical Heisenberg model without an external field which is defined by the Hamiltonian: \mathcal{H} = -\sum_{ij} J_{ij} \vec{s_i}\vec{s_j} where J_{ij} > 0 describes the coupling between the spins \vec{s}_i \in \mathbb{R}^3 on some lattice. (Is there a way to use tex...
  25. Haorong Wu

    A Heisenberg equations of Klein-Gordon Field in Space-Time

    Hi, there. I am reading An Introduction to Quantum Field Theory by Peskin and Schroeder. I am confused about some equations in section 2.4 The Klein-Gordon Field in Space-Time. It computes the Heisenberg equations of ##\phi \left ( x \right )## and ##\pi \left ( x \right)## as (in page 25) ##...
  26. T

    Heisenberg and Varying the Velocity

    Good Morning When we derive the Euler Lagrange equations using Hamilton's Principle, we make a point of varying the velocity and the position at the same time, (despite the fact that, normally, they are related through a derivative). I do understand that this is allowed: we are trying to find...
  27. Haorong Wu

    How to calculate an operator in the Heisenberg picture?

    I have some problems when calculating the operators in Heisenberg picture. First, ##\frac {dx} {dt} = \frac {1} {i \hbar} \left [ x, H \right ] = \frac {p} {m}##. Similarly, ##\frac {dp} {dt} = \frac {1} {i \hbar} \left [ p, H \right ] = - m \omega ^ 2 x##. These are coupled equations. I...
  28. MichPod

    I What did Heisenberg know about the measurement problem?

    While reading a book "Physics and Philosophy: The Revolution in Modern Science." by Werner Heisenberg, 1958, I was much surprised by the following passage near the end of Chapter 3: "The measuring device deserves this name only if it is in close contact with the rest of the world, if there is...
  29. LarryS

    I Quantum Measurement under Heisenberg Picture?

    When a quantum measurement occurs under the Schrodinger picture, the wave function collapses to one of the eigenvectors of the operator-observable and the value measured is the corresponding eigenvalue of that eigenvector. What happens during a quantum measurement under the Heisenberg picture...
  30. cemtu

    I Heisenberg Uncertainty: simple explanation required please

    why can't we know where electron goes after it was hit by light? Light has a travel direction, can't we assume that electron bounces to the same direction that the light was headed??
  31. K

    I What is the name for the Heisenberg uncertainty principle?

    In quantum mechanics the name is Uncertainty principle. But outside of QM, what is the name for those inequalities?
  32. PeterDonis

    A What is the Corrected Heisenberg Limit for Phase Estimation Measurements?

    A 2019 paper by Gorecki et al. derives an uncertainty principle limit that is larger than the conventional Heisenberg limit by a factor of ##\pi##: https://arxiv.org/abs/1907.05428 I'm wondering if any QM experts have seen this and what your thoughts are.
  33. J

    A Mean field theory in the Heisenberg model

    I have a problem about Heisenberg model.When applying mean field approximation,why does the average of spin flip terms be zero(<S+>=<S-> = 0 )? Thanks
  34. F

    I Interpretation of QM in the Heisenberg Picture

    This is in reference to a question, never fully resolved, posed here: https://www.physicsforums.com/threads/interpretation-of-the-heisenberg-picture-in-qm.816449/ The von Neumann postulates for Quantum Theory - Evolution (Schrödinger's equation) and Projection (Born's rule) are always framed...
  35. Haorong Wu

    The position and momentum operators for a free particle in Heisenberg picture

    Homework Statement From Griffiths GM 3rd p.266 Consider a free particle of mass ##m##. Show that the position and momentum operators in the Heisenberg picture are given by$$ {\hat x}_H \left( t \right) ={\hat x}_H \left( 0 \right) + \frac { {\hat p}_H \left( 0 \right) t} m $$ $$ {\hat p}_H...
  36. H

    I Symmetry transformation in Heisenberg vs Schrödinger Picture

    Symmetry transformations are changes in our point of view that preserve the possible outcomes of experiment: $$\Psi \rightarrow U(\Lambda) \Psi$$ In the Heisenberg picture, observables in a fixed reference frame evolve according to: $$P(t) = U^\dagger (t)PU(t)$$ while in the Schrodinger...
  37. M

    I Photons and Heisenberg's Uncertainty Principle

    To summarize, my current understanding of how Heisenberg's uncertainty principal works suggests that there would be a contradiction (somewhere down the line) with any way that it applies to (or doesn't apply to) photons, due to the fact that they must always travel the speed of light. I...
  38. Another

    I About the Heisenberg uncertainty principle

    heisenberg uncertainty principle ## Δx Δp ≥ ħ## where ##Δx = \sqrt{<\hat{x}^2>-<\hat{x}>^2}## ##Δp = \sqrt{<\hat{p}^2>-<\hat{p}>^2}## I don't know. Why ##Δx## equal to ## \sqrt{<\hat{x}^2>-<\hat{x}>^2} ## and ## Δp ## equal to ## \sqrt{<\hat{p}^2>-<\hat{p}>^2} ## What can I find out about...
  39. F

    I Heisenberg - Uncertainty principle - lifetime of a particle

    I have seen that the more a particle has a high energy, i.e ##E##, the more its lifetime is short, respecting so the uncertainty principle. But by the definition of this uncertainty principle : ##E\,\Delta t \geq \dfrac{\hbar}{2}##, I can write : ##\Delta t \geq \dfrac{\hbar}{2E}##, then...
  40. GiovanniNunziante

    A Derivation of the Heisenberg equation for electron density

    I'm studying plasmons from "Haken-Quantum Field Theory of Solids", and i need some help in the calculation of the equation of motion of eletrons' density \begin{equation} \hat{\rho}_{\overrightarrow{q}} = \frac{1}{\sqrt{V}} \sum_{\overrightarrow{k}}...
  41. renec112

    QM: Issues with parity of spherical harmonics and Heisenberg

    Hi physics forms! I'm practicing to for an Quantum mechanics exam, and i have a problem. 1. Homework Statement I have two problems, but it's all related to the same main task. I have a state for the Hydrogen: ## \Psi = \frac{1}{\sqrt{2}}(\psi_{100} + i \psi_{211})## where ## \psi_{nlm}##...
  42. E

    I How Does the Heisenberg Uncertainty Principle Relate to Statistics?

    to begin with I am a biophysicist so my question is very naive. It is my understanding that the Uncertainty Principle deals with a single event (particle). It is also my understanding that quantum physics contains a lot of statistics (probability). The question is: in the area of...
  43. e2m2a

    I Cosmological Redshift and Heisenberg Uncertainty Principle

    Has anyone conjectured that the redshift associated with Hubble's constant can be explained by Heisenberg's uncertainty principle? Another words, the further in space away from us a photon is emitted from a galaxy, the longer in time it takes for the photon to reach us. Since the photon has a...
  44. P

    I Heisenberg and the wave-particle dualism

    Hi! I am a bit confused about something Heisenberg said about the wave-particle dualism. In his book about physics and philosophy he wrote: "The dualism between the two complementary pictures - waves and particles - is also clearly brought out in the flexibility of the mathematical scheme. The...
  45. Derek P

    I Heisenberg Uncertainty vs Measurement Error

    Spun off from https://www.physicsforums.com/threads/is-quantum-physics-retro-deterministic.945431/#post-5984157. @Gerinski said: if we measure a particle's position at time X (not caring about its momentum) and we measure it again at a later time Y and we find it at some other position (again...
  46. Derek P

    I The inequality in the Heisenberg uncertainty relation

    I was musing about why the HUP is an inequality. If you analyse a wave packet the spatial frequency spectral width is inversely proportional to the spatial width. So there should be an equality such as Heisenberg's equation 3 in this paper. Has anyone got a simple explanation of where the...
  47. T

    B Understanding the Limits of Measurement in Quantum Mechanics

    Is it somehow possible to know both noncommutating properities of eg. a partcle, with using two indicators? Eg. two teams, with one is studing the momentum, and other one the position - then it's somehow impossible to exchange informations?
  48. Noora Alameri

    I Two dimenstional Heisenberg Hamiltonian for spin 1/2 system

    Hey everybody, I am trying to expand a system of seven qubits from one dimensional Hamiltonian to the two dimensional representation. I have the one dimensional representation and I don't know what to add to transform it from 1D to 2D representation. I would really appreciate your help and...
  49. Pickled_Gorilla

    What Is the Width of the Region on the Detector Hit by Neutrons?

    Homework Statement A collection of neutrons, nominally at rest, are confined in a region 1.0 nm wide on the x-axis at a height of 50 cm above a neutron detector. The neutrons are released and fall under the influence of gravity towards the detector which records the horizontal position of the...
  50. MichPod

    B Where is the mistake -- violation of Heisenberg uncertainty

    The following is kind of a semiclassical reasoning which goes along the style of the discussions between Bohr and Einstein in Solvay Conference. Suppose we have a single slit from which a particle may be emitted and, on a very large distance from it, a thin cloud chamber CC, which we use as a...
Back
Top