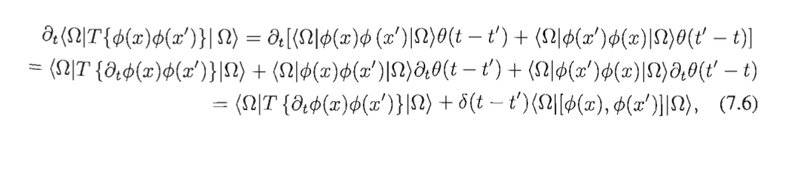SUMMARY
The discussion focuses on the derivation of Schwinger-Dyson equations, specifically addressing the confusion surrounding the appearance of the commutator in the final expression. Participants clarify that the delta functions emerge from Heaviside functions, and emphasize the importance of understanding the relationship between ##\theta(-t)## and ##\theta(t)##. The use of the chain rule for differentiation is highlighted as a critical step in resolving the confusion regarding the signs in the terms. Overall, the discussion provides clarity on the mathematical foundations necessary for deriving these equations.
PREREQUISITES
- Understanding of Schwinger-Dyson equations
- Familiarity with Heaviside and delta functions
- Knowledge of commutators and anticommutators in quantum field theory
- Proficiency in differentiation techniques, including the chain rule
NEXT STEPS
- Study the derivation process of Schwinger-Dyson equations in detail
- Learn about the properties and applications of Heaviside and delta functions
- Explore the role of commutators and anticommutators in quantum mechanics
- Review advanced differentiation techniques and their applications in physics
USEFUL FOR
This discussion is beneficial for theoretical physicists, graduate students in quantum field theory, and anyone interested in the mathematical foundations of particle physics.