Second Derivative Test for Local Extrema

[22990atinesh]

Suppose $f^{\prime\prime}$ is continuous on an open interval that contains x = c

1. If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)<0$, then $f$ has local maximum at x = c.
2. If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)>0$, then $f$ has local minimum at x = c.
3. If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)=0$, then the test fails. The function $f$ may have a local maximum, a local minimum, or neither.

I've a little doubt in point 3. I've come up with only 1 example for the possibility when

$f^{\prime}(c)=0$, $f^{\prime\prime}(c)=0$ and $f$ has neither local maximum or local minimum.

Ex: $f(x)=x^3$

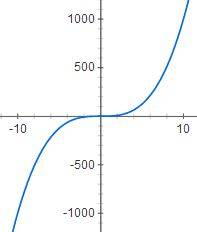
Please give examples for other two possibilities when

$f^{\prime}(c)=0$, $f^{\prime\prime}(c)=0$ and f has local maximum

$f^{\prime}(c)=0$ , $f^{\prime\prime}(c)=0$ and f has local minimum

 

[UltrafastPED]

When condition (3) occurs you can just take another derivative ... see
http://mathworld.wolfram.com/SecondDerivativeTest.html

And see the references.

 

[HallsofIvy]

For the first, f(x)= 1- x^4. For the second, f(x)= x^4.

 

[22990atinesh]

For the first, f(x)= 1- x^4. For the second, f(x)= x^4.

Thanx I get it