SUMMARY
The discussion focuses on converting a second-order ordinary differential equation into a system of first-order differential equations and expressing it in matrix form, referencing LM Hocking's book on Optimal Control. The user expresses confusion over discrepancies between their solution and the book's solution. It is concluded that the user's method is valid, with the primary difference being the definition of the variable x2, which affects the constants involved but does not alter the overall solution.
PREREQUISITES
- Understanding of second-order ordinary differential equations
- Familiarity with first-order differential equations
- Knowledge of matrix representation of systems of equations
- Basic concepts of optimal control theory
NEXT STEPS
- Study the conversion process from second-order to first-order differential equations
- Learn about matrix forms of differential equations
- Explore the implications of variable definitions in differential equations
- Review LM Hocking's Optimal Control for deeper insights on differential equations
USEFUL FOR
Students and professionals in mathematics, engineering, and physics who are working with differential equations, particularly those interested in optimal control theory and system dynamics.
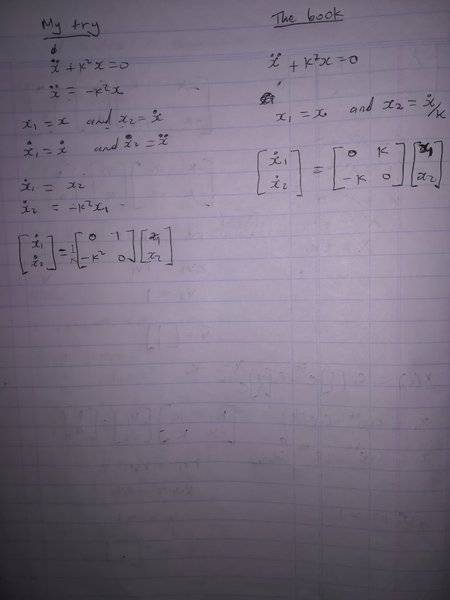 differs from the book?. I've attached both the book solution and mine. Thanks.
differs from the book?. I've attached both the book solution and mine. Thanks.