Second reflection angle of incidences in 3D

[vasanth]

TL;DR

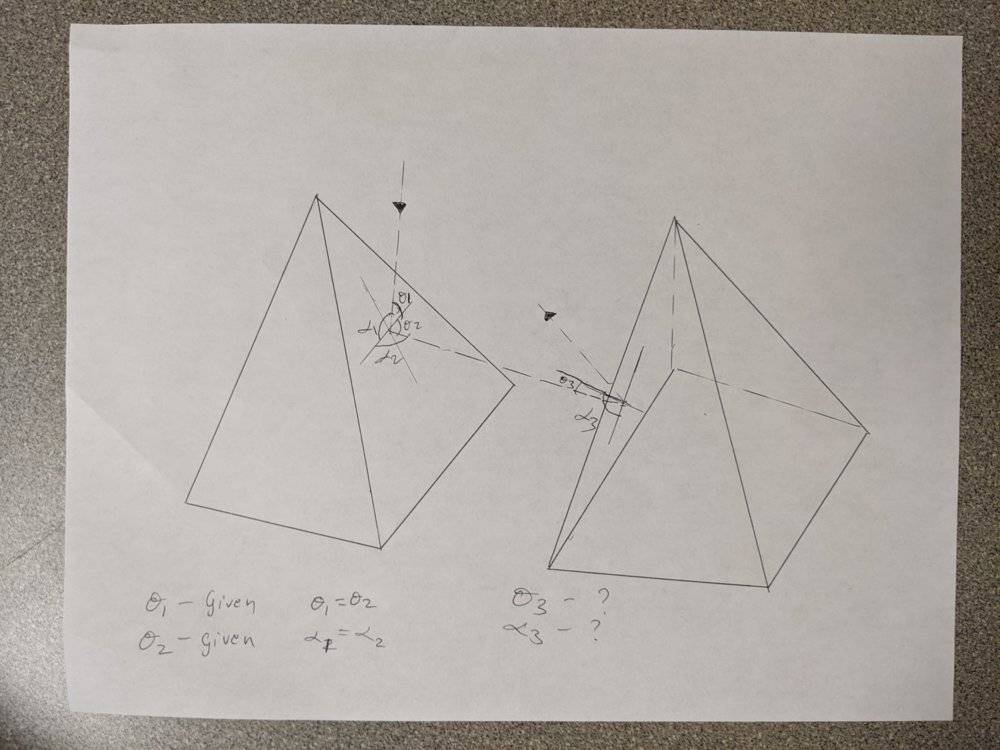
Given Theta1(angle of incidence) and alpha1(azimuth angle). how do we obtain the second reflection angle theta3 and alpha3?

Given Theta1(angle of incidence) and alpha1(azimuth angle). how do we obtain the second reflection angle theta3 and alpha3?
Assuming the surface to be a mirror reflection(theta1 = theta2). Need an equation when varied the incident angles we would obtain the second reflection angles or a method to do so.
please view the image for better understanding.

The pyramids are equally spaced of equal height and equal base length and same level(can also assume more number of pyramids in the x and y directions making z to be the height).
The angle of the pyramid can be a assumed(like 60 degree).

The given data is the first angles of incidence and reflection(assuming mirror reflection).
the unknown value is the second angles of incidence(forming or derived from the reflected or scattered)
also assuming the range of first incidence angles which will have a second reflection.

Thank you for your time and consideration.

 

[Lnewqban]

I don't have your answer, but I would assume both reflecting surfaces as being symmetrical to a vertical plane.
Consider that for each surface the in and out rays will be symmetrical to an imaginary line that is perpendicular to that surface.

If this is a real life practical problem, you will need dimensions, angles and distance between those pyramids, since you formula will be practical only within some limits, out of which the first reflection will not be able to reach the second surface.

I would experiment with making azimuth angle 90 degree first, then making angle of incidence constant and changing azimuth angle.
Best luck!