Semi-empirical mass formula and the pairing term

[rwooduk]

We have the formula for the mass of an atom:

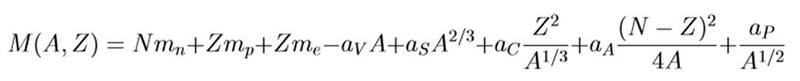
From our class notes I have:

By keeping A constant and varying Z there is generally only one stable nuclide for each odd value of A. We can show this by looking at the pairing term to show that odd A gives a single parabola with a single minimum.

Please could someone explain how he manages to get a single parabola from the pairing term? All I understand about the pairing term is that a_p<0 for Z,N even, even. a_p=0 for A odd and a_p>0 for Z,N odd, odd.

At a loss if anyone can help?

 

[ChrisVer]

Simple:
If A is odd, then N+Z is odd...
If N+Z is odd then one of them has to be even and the other odd (summing two odds or two evens will give an even number).
So a_P becomes zero and that term misses from the energy...
If A is even then a_P is non-zero... at this case you can have two different Z,N that give the same A which can achieve the least energy...

 

[rwooduk]

Simple:
If A is odd, then N+Z is odd...
If N+Z is odd then one of them has to be even and the other odd (summing two odds or two evens will give an even number).
So a_P becomes zero and that term misses from the energy...
If A is even then a_P is non-zero... at this case you can have two different Z,N that give the same A which can achieve the least energy...

Thanks that's really helpful and clears up the a_p values. I might be being really stupid here but I'll ask anyway, if the a_p term is zero then how is it a parabola? The only thing I can think of is that if the term is missing and you put N=A-Z into the equation you get some sort of quadratic in Z, which would be a parabola?

 

[ChrisVer]

yup, it's the quadratic equation in Z...
you can also check :
http://users.jyu.fi/~ptg/FYSN300/FYSN300_L3.pdf

 

[ChrisVer]

eg the figure in page 10 and its caption...

 

[rwooduk]

awesome, many thanks!