しおり's question at Yahoo Answers regarding Newton's method

[MarkFL]

Here is the question:

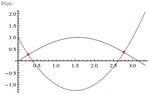
Use Newton's Method to find all roots of the equation sinx= x^2-3x+1 correct to six decimal places.?


I think first thing that I need to do is
let x^2-3x+1-sinx=0
then f(x)=x^2-3x+1-sinx

But I am stuck here...
I don't know how to get the interval and how to get x1

Please please explain how to solve this question for me.

Thank you!

I have posted a link there to this thread so the OP can see my work.

 

[MarkFL]

Hello しおり,

The first thing I would do is plot:

$$\sin(x)=x^2-3x+1$$

in order to get an idea where the roots are:

View attachment 1670

So, we see the smaller root is about $0.25$ and the larger root is about $2.75$.

Now, as you did, I would define:

$$f(x)=x^2-3x+1-\sin(x)$$

Hence:

$$f'(x)=2x-3-\cos(x)$$

Newton's method gives us the recursive algorithm:

$$x_{n+1}=x_n-\frac{f\left(x_n \right)}{f'\left(x_n \right)}$$

Using our function $f(x)$, we have:

$$x_{n+1}=x_n-\frac{x_n^2-3x_n+1-\sin\left(x_n \right)}{2x_n-3-\cos\left(x_n \right)}=\frac{2x_n^2-3x_n-x_n\cos\left(x_n \right)-\left(x_n^2-3x_n+1-\sin\left(x_n \right) \right)}{2x_n-3-\cos\left(x_n \right)}$$

$$x_{n+1}=\frac{x_n^2-x_n\cos\left(x_n \right)+\sin\left(x_n \right)-1}{2x_n-3-\cos\left(x_n \right)}$$

i) The smaller root: $$x_0=0.25$$

$$x_1\approx0.253025027391$$

$$x_2\approx0.268799448273$$

$$x_3\approx0.268881342724$$

$$x_4\approx0.268881344942$$

$$x_5\approx0.268881344942$$

ii) The larger root: $$x_0=2.75$$

$$x_1\approx2.77019710423$$

$$x_2\approx2.77005756932$$

$$x_3\approx2.77005756269$$

$$x_4\approx2.77005756269$$

Hence, the two roots of the given equation, rounded to 6 decimal places, are:

$$x\approx 0.268881,\,2.770058$$