mathlearn
- 331
- 0
I need help with the fourth part of this series of the questions,

Here's the copied figure
View attachment 5968
ii.
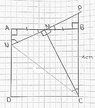
AM=MB (M midpoint)
NAM=MBP($90^\circ$)
AMN=BMP(vertically opposite)
$\therefore \triangle AMN \cong \triangle BMP \left(AAS\right)$iii.MN=MP (triangle AMN & triangle BMP congruent)
MC=MC (Common side)
NMC=CMP(Data)
$\triangle CMN \cong \triangle MCP \left(SAS\right)$
$\therefore \angle BCM= \angle MCN $
________________________________________________________________________
Now how are the triangles AMN & BMC equiangular ? One pair of equal angles would be
$\angle NAM$= $\angle MBC (90^\circ)$
Now what are the other two angles & what are the reasons for their equality ? (Thinking) (Smile)

Here's the copied figure
View attachment 5968
ii.
AM=MB (M midpoint)
NAM=MBP($90^\circ$)
AMN=BMP(vertically opposite)
$\therefore \triangle AMN \cong \triangle BMP \left(AAS\right)$iii.MN=MP (triangle AMN & triangle BMP congruent)
MC=MC (Common side)
NMC=CMP(Data)
$\triangle CMN \cong \triangle MCP \left(SAS\right)$
$\therefore \angle BCM= \angle MCN $
________________________________________________________________________
Now how are the triangles AMN & BMC equiangular ? One pair of equal angles would be
$\angle NAM$= $\angle MBC (90^\circ)$
Now what are the other two angles & what are the reasons for their equality ? (Thinking) (Smile)
Attachments
Last edited: