Show that for all n ∈ Z (>0), g(n) > f(n)

[gex]

Homework Statement

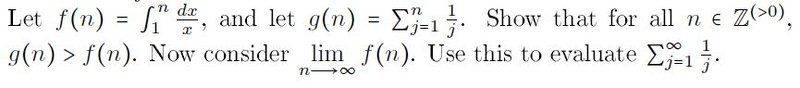
The attempt at a solution
Hi there, in an attempt to prove that g(n) is greater than f(n), I graphed both functions on the same axes and it is visually obvious that g(n) is greater than f(n), but I am not sure how I would go about proving this for all positive integers in a mathematically rigorous way. Any guidance is greatly appreciated.

 

[Mark44]

Thread moved. Please post questions involving integrals in the Calculus & Beyond section, not in the Precalc section.

I graphed both functions on the same axes and it is visually obvious that g(n) is greater than f(n),

Which "both functions" did you graph?
Think about f(n) as an area under a graph, and g(n) as the sum of areas of rectangles.

 

[gex]

Which "both functions" did you graph?

The above picture displays the graphs of f(n) and g(n) generated by https://www.desmos.com/calculator

Think about f(n) as an area under a graph, and g(n) as the sum of areas of rectangles.

I understand what you mean by thinking about f(n) as an area underneath a graph, but am quite unsure how g(n) represents the sum of areas of rectangles. I would appreciate some clarification this if possible, thank you.

 

[mfb]

Can you convert the sum for g(n) into an integral of a new function that matches the sum for each integer n?

I would shift the graph of the sum by 1/2 to the right, that makes it easier to see.

 

[Mark44]

Those aren't the right graphs. What I was talking about was graphing y = 1/x on the interval [1, n] for f, and comparing this to the graph of y = 1/j on the same interval for g, using a Riemann sum.

 

[gex]

Can you convert the sum for g(n) into an integral of a new function that matches the sum for each integer n?

I'm really not sure how I would go about doing that, I've never encountered such a thing before in my studies.

using a Riemann sum.

Sorry but I'm not quite sure what that is.

My teacher provided a hint for this question to the class that I don't understand either, and I'm not sure where this hint is supposed to lead me.

 

[Mark44]

Your teacher's hint is what I was suggesting in my post.
In the inequality in your teacher's hint, look at the interval [k, k+1] on the x-axis. Draw a rectangle whose width is 1 and whose height is 1/k. What's the area of this rectangle? (Easy question)
Also draw a curve from the point (k, 1/k) to the point (k + 1, 1/(k + 1)). The region under the curve is the integral in your teacher's hint. Which area is larger?

BTW, the graph you included in post #3 really is irrelevant in this problem, which is why I said earlier that you have drawn the wrong graphs.

 

[gex]

What's the area of this rectangle?

The area for such a rectangle would equal 1/k.

Which area is larger?

Substituting 1=k shows me that the area for the rectangle is larger than the region underneath the curve. Which makes sense as this shows that g(n) > f(n). But how would I go about proving this for all values of k ∈ Z ?

 

[Mark44]

The area for such a rectangle would equal 1/k.
Substituting 1=k shows me that the area for the rectangle is larger than the region underneath the curve. Which makes sense as this shows that g(n) > f(n). But how would I go about proving this for all values of k ∈ Z ?

Pick an arbitrary interval, [k, k + 1]. If g(x) > f(x) is true on an arbitrary interval, it's true for each one of them.

 

[gex]

Pick an arbitrary interval, [k, k + 1]. If g(x) > f(x) is true on an arbitrary interval, it's true for each one of them.

Thank you for your help Mark, I finally solved the problem :)